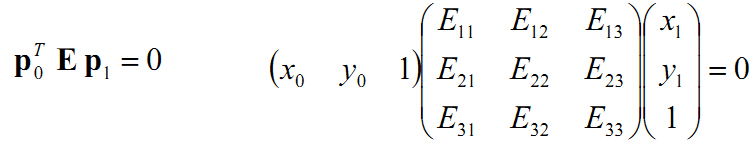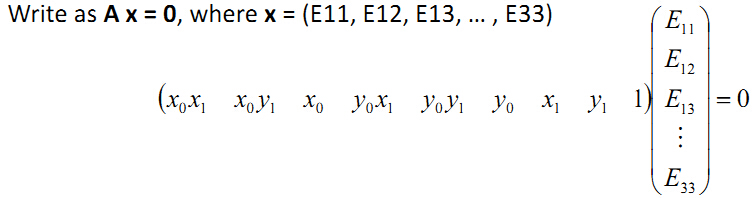在讲解恢复R,T前，稍微提一下特征点匹配的方法。
    常见的有如下两种方式： 
    1. 计算特征点，然后计算特征描述子，通过描述子来进行匹配，优点准确度高，缺点是描述子计算量大。 
    2. 光流法：在第一幅图中检测特征点，使用光流法(Lucas Kanade method)对这些特征点进行跟踪，
       得到这些特征点在第二幅图像中的位置，得到的位置可能和真实特征点所对应的位置有偏差。
       所以通常的做法是对第二幅图也检测特征点，如果检测到的特征点位置和光流法预测的位置靠近，
       那就认为这个特征点和第一幅图中的对应。
       在相邻时刻光照条件几乎不变的条件下（特别是单目slam的情形），
       光流法匹配是个不错的选择，它不需要计算特征描述子，计算量更小。

    对极几何原理：
    两个摄像机的光心C0、C1，三维空间中一点P，在两幅图像中的位置为p0、p1（相当于上面的 x1, x2）。
    像素点 u1，u2
    p0 = inv(K) * u0
    p1 = inv(K) * u1
    
          x0    (u0x - cx) / fx 
    p0 =  y0 =  (u0y - cy) / fy
           1     1
           
          x1    (u1x - cx) / fx 
    p1 =  y1 =  (u1y - cy) / fy
           1     1        
    
    如下图所示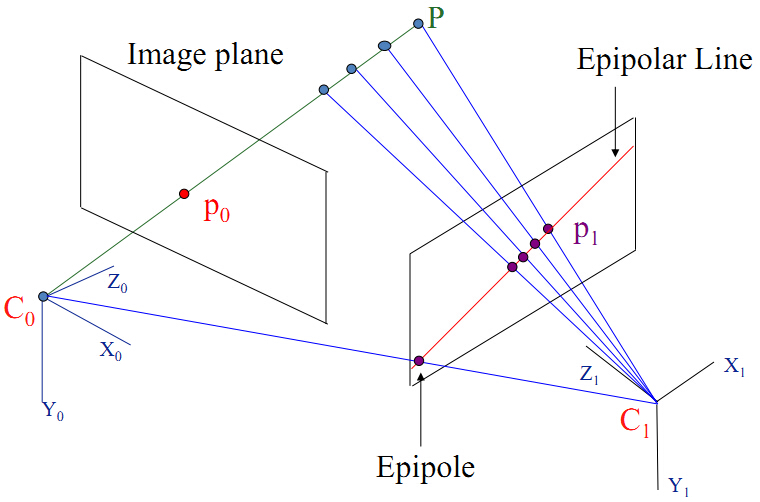： ![](https://img-blog.csdn.net/20160228210635964)

    由于C0、C1、P三点共面，得到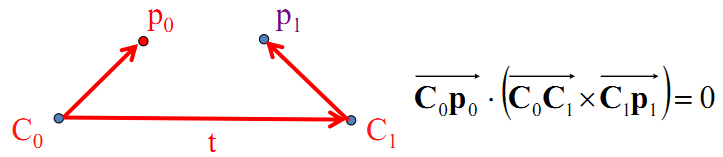：  ![](https://img-blog.csdn.net/20160228213615018)

     这时，由共面得到的向量方程可写成：  
     p0 *(t 叉乘 R * p1)
     其中，
     t是两个摄像机光心的平移量;
     R是从坐标系C1到坐标系C0的旋转变换，
     p1左乘旋转矩阵R的目的是把向量p1从C1坐标系下旋转到C0坐标系下(统一表示)。
     
     一个向量a叉乘一个向量b，
     可以表示为一个反对称矩阵乘以向量b的形式，
     这时由向量a=(a1,a2,a3) 表示的反对称矩阵(skew symmetric matrix)如下: 
     
           0  -a3  a2
     ax =  a3  0  -a1
          -a2  a1   0 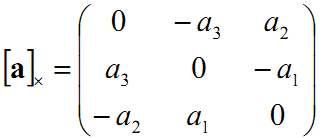![](https://img-blog.csdn.net/20160228220006072)

    所以把括号去掉的话，p0 需要变成 1*3的行向量形式
    才可以与 3*3的 反对称矩阵相乘
    
    p0转置 * t叉乘 * R * P1
    
   我们把  t叉乘 * R  = E 写成
   
   p0转置 * E * P1

    本征矩阵E的性质：          一个3x3的矩阵是本征矩阵的充要条件是对它奇异值分解后，
    它有两个相等的奇异值，并且第三个奇异值为0。
    牢记这个性质，它在实际求解本征矩阵时有很重要的意义 .
    
   计算本征矩阵E、尺度scale的来由:
   将上述矩阵相乘的形式拆开得到 ：

    上面这个方程左边进行任意缩放都不会影响方程的解： 
    
   (x0x1 x0y1 x0 y0x1 y0y1 y0 x1 y1 1)*E33(E11/E33 ... E32/E33 1) = 0
   所以E虽然有9个未知数，但是有一个变量E33可以看做是缩放因子，
   因此实际只有8个未知量，这里就是尺度scale的来由，后面会进一步分析这个尺度。
   
   AX=0，x有8个未知量，需要A的秩等于8，所以至少需要8对匹配点,应为有可能有两个约束是可以变成一个的，
   点可能在同一条线上，或者所有点在同一个面上的情况，这时候就存在多解,得到的值可能不对。
   
   对矩阵A进行奇异值SVD分解，可以得到A

    *                    f1   f2    f3      u1
    *   (u2 v2 1)    *   f4   f5    f6  *   v1  = 0  
    *                    f7   f8    f9       1
    按照矩阵乘法展开：
    a1 = f1*u2 + f4*v2 + f7;
    b1 = f2*u2 + f5*v2 + f8;
    c1 = f3*u2 + f6*v2 + f9;
    得到：
    a1*u1+ b1*v1 + c1= 0
    展开：
    f1*u2*u1 + f2*u2*v1 + f3*u2 + f4*v2*u1 + f5*v2*v1 + f6*v2 + f7*u1 + f8*v1 + f9*1 = 0
    写成矩阵形式：
    [u1*u2 v1*u2 u2 u1*v2 v1*v2 v2 u1 v1 1]*[f1 f2 f3 f4 f5 f6 f7 f8 f9]转置 = 0
    f 9个变量，1个尺度因子，相当于8个变量
    一个点对，得到一个约束方程
    需要8个点对，得到8个约束方程，来求解8个变量
    A*f = 0
    所以F虽然有9个未知数，但是有一个变量f9可以看做是缩放因子，
    因此实际只有8个未知量，这里就是尺度scale的来由，后面会进一步分析这个尺度。 

    上面这个方程的解就是矩阵A进行SVD分解A=UΣV转置 后，V矩阵是最右边那一列的值f。
    另外如果这些匹配点都在一个平面上那就会出现A的秩小于8的情况，
    这时会出现多解，会让你计算的E/F可能是错误的。    

    A * f = 0 求 f   
    奇异值分解F 基础矩阵 且其秩为2 
    需要再奇异值分解 后 取对角矩阵 秩为2 后在合成F

    cv::Mat u,w,vt;
    cv::SVDecomp(A,w,u,vt,cv::SVD::MODIFY_A | cv::SVD::FULL_UV);// A = w * u * vt
    cv::Mat Fpre = vt.row(8).reshape(0, 3);// F 基础矩阵的秩为2 需要在分解 后 取对角矩阵 秩为2 在合成F
    cv::SVDecomp(Fpre,w,u,vt,cv::SVD::MODIFY_A | cv::SVD::FULL_UV);
    w.at<float>(2)=0;//  基础矩阵的秩为2，重要的约束条件
    F =  u * cv::Mat::diag(w)  * vt;// 在合成F

    从基本矩阵恢复 旋转矩阵R 和 平移向量t
            F =  K转置逆 * E * K逆
    本质矩阵 E  =  K转置 * F * K =  t 叉乘 R

    从本质矩阵恢复 旋转矩阵R 和 平移向量t
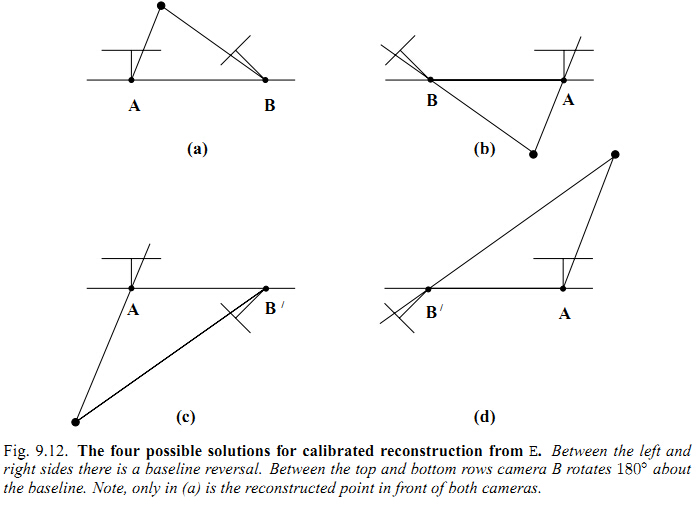
    恢复时有四种假设 并验证得到其中一个可行的解
    本质矩阵E = t 叉乘 R 恢复变换矩阵R,t的时候，有四种情况，但是只有一种是正确的。
    而判断正确的标准，
    就是按照这个R,t 计算出来的深度值(两个坐标系下的三维坐标的Z值)都是正值，
    因为相机正前方为Z轴正方向。
    三角变换计算三维坐标可按后面的方法计算。

    本征矩阵的性质： 
    一个3x3的矩阵是本征矩阵的充要条件是对它奇异值分解后，
    它有两个相等的奇异值，
    并且第三个奇异值为0。
    牢记这个性质，它在实际求解本征矩阵时有很重要的意义。

    计算本征矩阵E的八点法，大家也可以去看看wiki的详细说明 

    有本质矩阵E 恢复 R,t
    从R,T的计算公式中可以看到R,T都有两种情况，
    组合起来R,T有4种组合方式。
    由于一组R,T就决定了摄像机光心坐标系C的位姿，
    所以选择正确R、T的方式就是，把所有特征点的深度计算出来，
    看深度值是不是都大于0，深度都大于0的那组R,T就是正确的。

    用单应变换矩阵H或者本质矩阵E 求解得到相邻两帧的变换矩阵R,t后就可是使用类似双目的
    三角测距原理来得到深度。 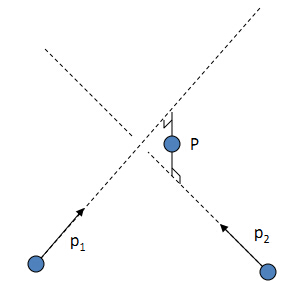![](https://img-blog.csdn.net/20160301171837557)

    上图中的物理物理中的点    P =[X,Y,Z,1]
    在两相机归一化平面下的点  x1  x2  [x,y,z]
    在两相机像素平面上的点    p1, p2，匹配点对　[u,v,1]
    p1 = k × [R1 t1] × P   
    左乘　k逆 × p1 =  [R1 t1] × P   
    得到　x1 = T1 × P   
    计算　x1叉乘x1 =  x1叉乘T1 × P = 0
    这里 T1 = [I, 0 0 0] 为单位矩阵。
    p2 = k × [R2 t2]  × P    
    左乘　k逆 × p2 =  [R2 t2] × P    
    得到　x2 = T2 × P   
    消去　x2叉乘x2 =  x2叉乘T2 × P = 0      
    式中：
     x1 = k逆 × p1 ，
     x2 = k逆 × p2 ， 
     T2= [R, t]为帧1变换到帧2的 已知
    得到两个方程
    x1叉乘T1 × P = 0
     x2叉乘T2 × P = 0 
     写成矩阵形式　A*P = 0
     A = [x1叉乘T1; x2叉乘T2]
    这又是一个要用最小二乘求解的线性方程方程组 ,和求本征矩阵一样，
    计算矩阵A的SVD分解，然后奇异值最小的那个奇异向量就是三维坐标P的解。
    P是3维齐次坐标，需要除以第四个尺度因子 归一化. 
    [U,D,V] = svd(A);
    P = V[:,4] 最后一列
    P = P/P(4)；// 归一化
    以上也是由本质矩阵E = t 叉乘 R 恢复变换矩阵R,t的时候，有四种情况，但是只有一种是正确的。
    而判断正确的标准，就是按照这个R,t 计算出来的深度值都是正值，因为相机正前方为Z轴正方向。

    我们知道通过两帧图像的匹配点就可以计算出这一点的深度值，
    如果有多幅匹配的图像，那就能计算出这一点的多个深度值。
    一幅图像对应另外n幅图像，可以看作为n个深度传感器，
    把得到点的深度信息的问题看作是有噪声的多传感器数据融合的问题，
    使用Gaussian Uniform mixture model(高斯均值混合模型)来对这一问题进行建模，
    假设好的测量值符合正态分布，好的测量值的比例为pi,
    噪声符合均匀分布，噪声比例为1-pi 使用贝叶斯方法不断更新这个模型，
    让点的深度（也就是正态分布中的均值参数）和好的测量值的比例pi收敛到真实值。　

    好的测量值符合正态分布
    噪声符合均匀分布，
    使用贝叶斯方法(最大后验概率)更新，这是SVO中深度滤波的部分。

    好的测量值和噪声均符合高斯分布，使用卡尔曼滤波来进行深度测量值的滤波
    这是LSD中的方法。

    这就像对同一个状态变量我们进行了多次测量，
    因此，可以用贝叶斯估计来对多个测量值进行融合，
    使得估计的不确定性缩小。
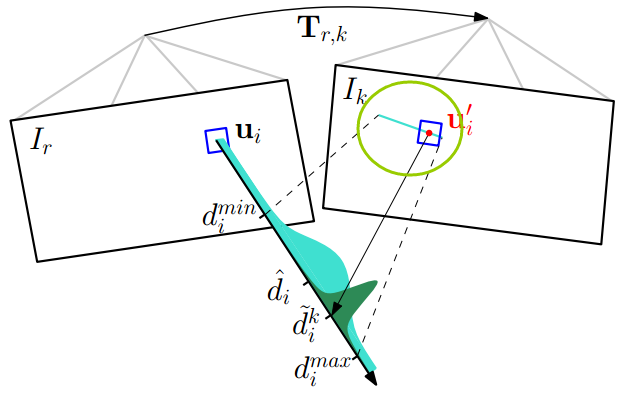
    如下图所示：

    一开始深度估计的不确定性较大(浅绿色部分)，
    通过三角化得到一个深度估计值以后，
    能够极大的缩小这个不确定性(墨绿色部分)。