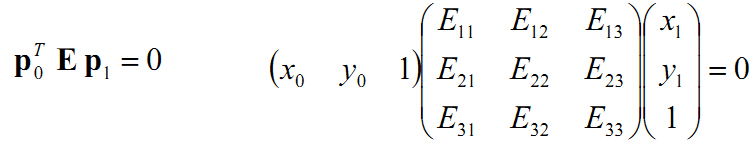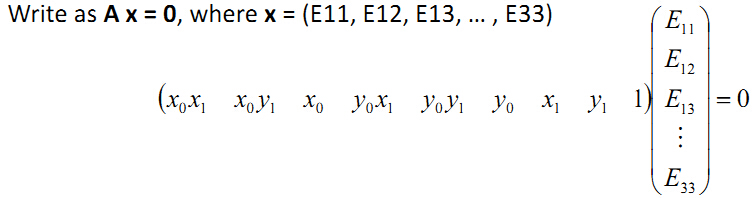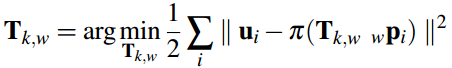svo: semi-direct visual odometry 半直接视觉里程计
svo: semi-direct visual odometry 论文解析
1.1为什么叫半直接法?
我们知道,VSLAM有直接法和特征点法两大类。直接法和特征点法,在帧间VO阶段的不同在于,
直接法:提取梯度纹理特征明显的像素,帧间VO是靠图像对齐,即通过
最小化像素灰度差函数来优化帧间位姿。
特征点法:提取特征点(通常是角点),帧间VO靠PNP,即缩小在后帧图像上,
重投影点与特征匹配点距离误差,来优化帧间位姿。
而SVO是这样干的:
提取稀疏特征点(类似特征点法),帧间VO用图像对齐(类似于直接法),
SVO结合了直接法和特征点法,因此,称它为半直接法。
SVO主要干了两件事,
<1>跟踪
<2>深度滤波
深度滤波是我们常说的建图(Mapping)部分。
1.2.1跟踪部分
跟踪部分干的事情是:初始化位姿,估计和优化位姿(分别对应于帧间VO和局部地图优化)。
初始化位姿:
用KLT光流法找匹配,然后恢复H矩阵。初始化思想是这样的,
第一帧上提取的特征点,作为关键帧,后来的帧不断用KLT与第一帧匹配,
直到匹配到的特征点平均视差比较大,就认为初始化成功,计算对应特征点的深度,
与此对应的帧作为第二帧。之后进入正常工作模式,即估计和优化位姿。
正常工作模式:
首先,通过和上一帧进行对齐,求取初始位姿;
然后,建立局部地图,通过优化局部地图和当前帧的投影灰度块误差,来优化当前位姿;
最后,判断此帧是否是关键帧,如果为关键帧就提取新的特征点。
经过以上四个步骤,完成一帧的处理。如果在CMakeLists里打开了HAVE_G2O的选项,
代码隔一段时间还会BA,不过非常慢。
1.2.2深度滤波部分
深度滤波部分主要任务是完成估计特征点的深度信息。
深度滤波和跟踪部分相互依赖,因为深度滤波是以相机位姿已知为前提进行的,
而跟踪部分又依靠深度滤波的结果(较准确的三维点),完成位姿的估计。
乍一看,这是个鸡生蛋,蛋生鸡的问题,既然两者循环迭代,总得有个起始点。
其实,单目的slam在启动时需要初始化,而这个初始化就提供粗糙的帧间位姿,
以便于深度滤波和跟踪部分的迭代。
当深度可以用后(称之为收敛),把它放入地图里,用于跟踪。
1.2.3为什么叫VO
这个得从SVO干的事来说,它既没有闭环检测,也没有重定位(SVO的重定位太。。。),
它干的事只要是定位,比较符合视觉里程计(VO)的特点。
ORBSLAM算是目前性能最好的开源算法,这些功能它都有,因此算一个比较完整的VSLAM算法。
1.2.4 svo怎么样
优点:是比较快,如果你跑代码的时候发现很容易跟丢,可以修改这几个配置参数:
quality_min_fts:匹配到的最小特征点。
quality_max_drop_fts:容许相邻帧匹配到特征点的最大落差。
缺点:缺点是比较明显的
和ORBSLAM相比。
<1>由于位姿的估计和优化全是靠灰度匹配,这就导致了系统对光照的鲁棒性不足。
<2>对快速运动鲁棒性性不足。直接法都似这个样子。。可以加入IMU改善。
<3>没有重定位和闭环检测功能。
如果把此工程修改成RGBD的模式后,鲁棒性和精度明显提高,近似于ORBSLAM的RGBD模式。
半直接法解析
SVO 从名字来看,是半直接视觉里程计,
所谓半直接是指通过对图像中的特征点图像块进行直接匹配来获取相机位姿,
而不像直接匹配法那样对整个图像(根据灰度梯度大小筛选需要匹配的点)使用直接匹配。
整幅图像的直接匹配法常见于RGBD传感器,因为RGBD传感器能获取整幅图像的深度。
虽然semi-direct方法使用了特征,但它的思路主要还是通过direct method来获取位姿,这和特征点法feature-method不一样。
同时,semi-direct方法和direct method不同的是它利用特征块的配准来对direct method估计的位姿进行优化。
和常规的单目一样,SVO算法分成两部分: 位姿估计,深度估计 ## 直接法
使用图像中具有灰度梯度大的点 使用极线搜索(线段匹配)获得匹配点对,
参考帧根据深度信息建立3d点,
按照3d-2d匹配,
将3d点按照变换矩阵以及相机内参数投影到当前帧,获取亚像素灰度值,
和原有的匹配点做差,得到灰度差值,使用加权LM算法进行优化,得到变换矩阵[R t]。 ## 半直接法
利用特征块的配准来对direct method估计的位姿进行优化。 ## 特征点法
使用ORB等特征提取方法,确定两幅图像中的匹配点对(特征点快匹配),对应同一个物理空间中的点
使用 单应矩阵H / 或者本质矩阵F求解 变换矩阵[R t]
2D-2D点三角化 得到对应的 三维点坐标
也可转化到 相机归一化平面下的点 x1 x2
p1 = k × [R1 t1] × D k逆 × p1 = [R1 t1] × D x1 = T1 × D x1叉乘x1 = x1叉乘T1 × D = 0
p2 = k × [ R2 t2] × D k逆 × p2 = [R2 t2] × D x2 = T2 × D x2叉乘x2 = x2叉乘T2 × D = 0
式中:x1 = k逆 × p1 ,x2 = k逆 × p2 , T= [R, t] 已知
可以求解D
D是3维齐次坐标,需要除以第四个尺度因子 归一化 ### 特征点匹配
在讲解恢复R,T前,稍微提一下特征点匹配的方法。
常见的有如下两种方式:
1. 计算特征点,然后计算特征描述子,通过描述子来进行匹配,优点准确度高,缺点是描述子计算量大。
2. 光流法:在第一幅图中检测特征点,使用光流法(Lucas Kanade method)对这些特征点进行跟踪,
得到这些特征点在第二幅图像中的位置,得到的位置可能和真实特征点所对应的位置有偏差。
所以通常的做法是对第二幅图也检测特征点,如果检测到的特征点位置和光流法预测的位置靠近,
那就认为这个特征点和第一幅图中的对应。
在相邻时刻光照条件几乎不变的条件下(特别是单目slam的情形),
光流法匹配是个不错的选择,它不需要计算特征描述子,计算量更小。
单应矩阵H 恢复变换矩阵 R, t
p2 = H12 * p1 4对点 A*h = 0 奇异值分解 A 得到 单元矩阵 H , T = K 逆 * H21*K
展开成矩阵形式:
u2 h1 h2 h3 u1
v2 = h4 h5 h6 * v1
1 h7 h8 h9 1
按矩阵乘法展开:
u2 = (h1*u1 + h2*v1 + h3) /( h7*u1 + h8*v1 + h9)
v2 = (h4*u1 + h5*v1 + h6) /( h7*u1 + h8*v1 + h9)
将分母移到另一边,两边再做减法
-((h4*u1 + h5*v1 + h6) - ( h7*u1*v2 + h8*v1*v2 + h9*v2))=0 式子为0 左侧加 - 号不变
h1*u1 + h2*v1 + h3 - ( h7*u1*u2 + h8*v1*u2 + h9*u2)=0
写成关于 H的矩阵形式:
0 0 0 0 -u1 -v1 -1 u1*v2 v1*v2 v2
u1 v1 1 0 0 0 0 -u1*u2 -v1*u2 -u2 * (h1 h2 h3 h4 h5 h6 h7 h8 h9)转置 = 0
h1~h9 9个变量一个尺度因子,相当于8个自由变量
一对点 2个约束
4对点 8个约束 求解8个变量
A*h = 0 奇异值分解 A 得到 单元矩阵 H
cv::SVDecomp(A,w,u,vt,cv::SVD::MODIFY_A | cv::SVD::FULL_UV);// 奇异值分解
H = vt.row(8).reshape(0, 3);// v的最后一列
单应矩阵恢复 旋转矩阵 R 和平移向量t
p2 = H21 * p1 = H21 * KP
p2 = K( RP + t) = KTP = H21 * KP
T = K 逆 * H21*K
本质矩阵F求解 变换矩阵[R t] p2转置 * F * p1 = 0
基本矩阵的获得
空间点 P 两相机 像素点对 p1 p2 两相机 归一化平面上的点对 x1 x2 与P点对应
p1 = KP
p2 = K( RP + t)
x1 = K逆* p1 = P
x2 = K逆* p2 = ( RP + t) = R * x1 + t
消去t(同一个变量和自己叉乘得到0向量)
t 叉乘 x2 = t 叉乘 R * x1
再消去等式右边
x2转置 * t 叉乘 x2 = 0 = x2转置 * t 叉乘 R * x1
得到 :
x2转置 * t 叉乘 R * x1 = x2转置 * E * x1 = 0 本质矩阵
也可以写成:
p2转置 * K 转置逆 * t 叉乘 R * K逆 * p1 = p2转置 * F * p1 = 0 基本矩阵
几何知识参考
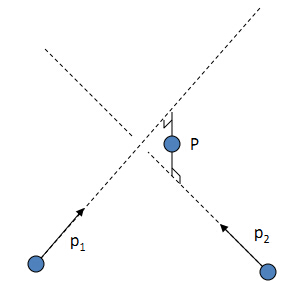
对极几何原理:
两个摄像机的光心C0、C1,三维空间中一点P,在两幅图像中的位置为p0、p1(相当于上面的 x1, x2)。
像素点 u1,u2
p0 = inv(K) * u0
p1 = inv(K) * u1
x0 (u0x - cx) / fx
p0 = y0 = (u0y - cy) / fy
1 1
x1 (u1x - cx) / fx
p1 = y1 = (u1y - cy) / fy
1 1
如下图所示: 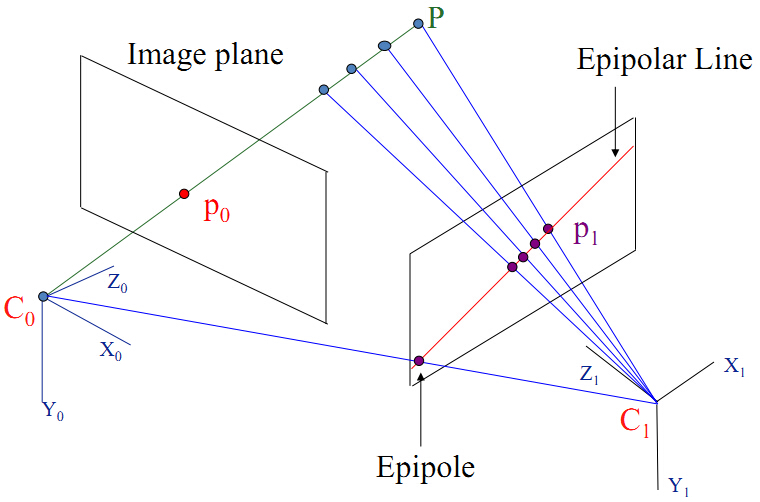
由于C0、C1、P三点共面,得到: 
这时,由共面得到的向量方程可写成:
p0 *(t 叉乘 R * p1)
其中,
t是两个摄像机光心的平移量;
R是从坐标系C1到坐标系C0的旋转变换,
p1左乘旋转矩阵R的目的是把向量p1从C1坐标系下旋转到C0坐标系下(统一表示)。
一个向量a叉乘一个向量b,
可以表示为一个反对称矩阵乘以向量b的形式,
这时由向量a=(a1,a2,a3) 表示的反对称矩阵(skew symmetric matrix)如下:
0 -a3 a2
ax = a3 0 -a1
-a2 a1 0 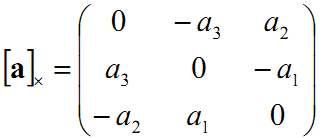
所以把括号去掉的话,p0 需要变成 1*3的行向量形式
才可以与 3*3的 反对称矩阵相乘
p0转置 * t叉乘 * R * P1
我们把 t叉乘 * R = E 写成
p0转置 * E * P1
本征矩阵E的性质: 一个3x3的矩阵是本征矩阵的充要条件是对它奇异值分解后,
它有两个相等的奇异值,并且第三个奇异值为0。
牢记这个性质,它在实际求解本征矩阵时有很重要的意义 .
计算本征矩阵E、尺度scale的来由:
将上述矩阵相乘的形式拆开得到 :
上面这个方程左边进行任意缩放都不会影响方程的解:
(x0x1 x0y1 x0 y0x1 y0y1 y0 x1 y1 1)*E33(E11/E33 ... E32/E33 1) = 0
所以E虽然有9个未知数,但是有一个变量E33可以看做是缩放因子,
因此实际只有8个未知量,这里就是尺度scale的来由,后面会进一步分析这个尺度。
AX=0,x有8个未知量,需要A的秩等于8,所以至少需要8对匹配点,应为有可能有两个约束是可以变成一个的,
点可能在同一条线上,或者所有点在同一个面上的情况,这时候就存在多解,得到的值可能不对。
对矩阵A进行奇异值SVD分解,可以得到A
#### p2转置 * F * p1 = 0 8点对8个约束求解得到F
* f1 f2 f3 u1
* (u2 v2 1) * f4 f5 f6 * v1 = 0
* f7 f8 f9 1
按照矩阵乘法展开:
a1 = f1*u2 + f4*v2 + f7;
b1 = f2*u2 + f5*v2 + f8;
c1 = f3*u2 + f6*v2 + f9;
得到:
a1*u1+ b1*v1 + c1= 0
展开:
f1*u2*u1 + f2*u2*v1 + f3*u2 + f4*v2*u1 + f5*v2*v1 + f6*v2 + f7*u1 + f8*v1 + f9*1 = 0
写成矩阵形式:
[u1*u2 v1*u2 u2 u1*v2 v1*v2 v2 u1 v1 1]*[f1 f2 f3 f4 f5 f6 f7 f8 f9]转置 = 0
f 9个变量,1个尺度因子,相当于8个变量
一个点对,得到一个约束方程
需要8个点对,得到8个约束方程,来求解8个变量
A*f = 0
所以F虽然有9个未知数,但是有一个变量f9可以看做是缩放因子,
因此实际只有8个未知量,这里就是尺度scale的来由,后面会进一步分析这个尺度。
上面这个方程的解就是矩阵A进行SVD分解A=UΣV转置 后,V矩阵是最右边那一列的值f。
另外如果这些匹配点都在一个平面上那就会出现A的秩小于8的情况,这时会出现多解,会让你计算的E/F可能是错误的。
A * f = 0 求 f
奇异值分解F 基础矩阵 且其秩为2
需要再奇异值分解 后 取对角矩阵 秩为2 后在合成F
cv::Mat u,w,vt;
cv::SVDecomp(A,w,u,vt,cv::SVD::MODIFY_A | cv::SVD::FULL_UV);// A = w * u * vt
cv::Mat Fpre = vt.row(8).reshape(0, 3);// F 基础矩阵的秩为2 需要在分解 后 取对角矩阵 秩为2 在合成F
cv::SVDecomp(Fpre,w,u,vt,cv::SVD::MODIFY_A | cv::SVD::FULL_UV);
w.at<float>(2)=0;// 基础矩阵的秩为2,重要的约束条件
F = u * cv::Mat::diag(w) * vt;// 在合成F
从基本矩阵恢复 旋转矩阵R 和 平移向量t
F = K转置逆 * E * K逆
本质矩阵 E = K转置 * F * K = t 叉乘 R
从本质矩阵恢复 旋转矩阵R 和 平移向量t
恢复时有四种假设 并验证得到其中一个可行的解
本征矩阵的性质:
一个3x3的矩阵是本征矩阵的充要条件是对它奇异值分解后,
它有两个相等的奇异值,
并且第三个奇异值为0。
牢记这个性质,它在实际求解本征矩阵时有很重要的意义。
计算本征矩阵E的八点法,大家也可以去看看wiki的详细说明
有本质矩阵E 恢复 R,t
从R,T的计算公式中可以看到R,T都有两种情况,
组合起来R,T有4种组合方式。
由于一组R,T就决定了摄像机光心坐标系C的位姿,
所以选择正确R、T的方式就是,把所有特征点的深度计算出来,
看深度值是不是都大于0,深度都大于0的那组R,T就是正确的。 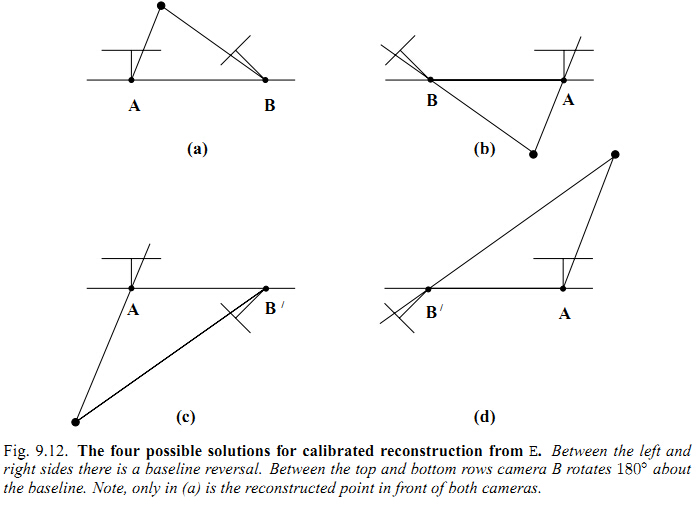
以上的解法 在 orbslam2中有很好的代码解法
尺度问题
这个图简单明了的演示了这种平移缩放作用。
从图中也可以看出,由于尺度scale的关系,
不同尺度的F得到不同的t,决定了以后计算点P的深度也是不同的,
所以恢复的物体深度也是跟尺度scale有关的,
这就是论文中常说的结构恢复structure reconstruction,
只是恢复了物体的结构框架,而不是实际意义的物体尺寸。并
且要十分注意,每两对图像计算E并恢复R,T时,他们的尺度都不是一样的,
本来是同一点,在不同尺寸下,深度不一样了,这时候地图map它最头痛了,所以这个尺度需要统一。
那么如何让scale之间统一呢?如果你一直采用这种2d-2d匹配计算位姿的方式,那每次计算的t都是在不同尺度下的,
一种方法使得相邻位姿间的不同的尺度s经过缩放进行统一。
我们已经知道出现尺度不一致是由于每次都是用这种计算本征矩阵的方式,而尺度就是在计算E时产生的。
所以尺度统一的另一种思路就是后续的位姿估计我不用这种2d-2d计算本征E的方式了。
也就说你通过最开始的两帧图像计算E恢复了R,T,
并通过三角法计算出了深度,那我就有了场景点的3D坐标,
后续的视频序列就可以通过3Dto2d(opencv里的solvePnp)来进行位姿估计
,这样后续的视频序列就不用计算本征矩阵从而绕过了尺度,
所以后续的视频序列的位姿和最开始的两帧的尺度是一样的了。
但是,这样计算又会产生新的问题–scale drift尺度漂移。
因为,两帧间的位姿总会出现误差,这些误差积累以后,
使得尺度不再统一了,
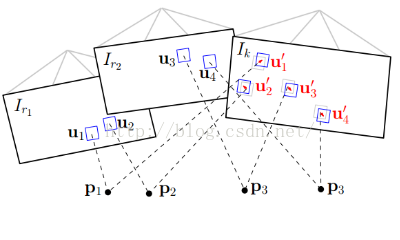
如下图所示: 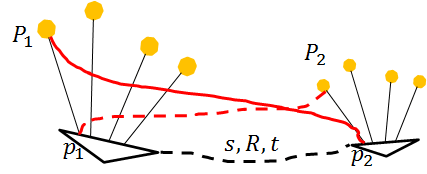
随着相机位姿误差的积累,地图中的四个点在第二帧的位置相对于第一帧中来说像是缩小了一样。
位姿误差累计导致尺度漂移这一点,对照上面讲尺度不确定问题时的那个图就很容易理解。
关于如何纠正这个scale drift的问题很多单目slam里都提到了,所以这里不再深入。
Features特征, Tracking跟踪, Essential Matrix本质矩阵, and RANSAC随机采样序列一致性
Stereo Visual Odometry 双目视觉里程计
Dense mapping: KinectFusion and DTAM
Kintinuous: Reconstruction of an Apartment ICP+RGBD
和常规的单目一样,SVO算法分成两部分: 位姿估计,深度估计
1. 位姿估计 motion estimation
svo 方法中motion estimation的步骤可以简单概括如下:
a) 相邻帧 2d-2d--->3d-2d匹配,最小化重投影误差计算R,t
对稀疏的特征块使用direct method 配准,获取相机位姿;
SE3跟踪详见lsd_slam中的方法。
参考帧2d点由逆深度得到3d点,进行3d-2d点像素误差匹配,3d点反投影到当前帧像素平面,和2d点的灰度误差
使用误差加权LM算法优化得到位姿。
b) 3d点反向追踪,获取参考关键帧像素位置--->放射变换----> 当前帧像素位置差值--->优化特征块在 当前帧中的位置
优化 3d-2d特征块匹配关系
通过获取的 位姿预测参考帧 中 的特征块在 当前帧中的位置,
由于深度估计的不准导致获取的位姿也存在偏差,从而使得预测的特征块位置不准。
由于预测的特征块位置和真实位置很近,所以可以使用牛顿迭代法对这个特征块的预测位置进行优化。
c) 使用优化后的 3d-2d特征块匹配关系, 再次使用直接法, 来对相机位姿(pose)以及特征点位置(structure)进行反向优化。
特征块的预测位置得到优化,说明之前使用直接法预测的有问题。
利用这个优化后的特征块预测位置,再次使用直接法,
对相机位姿(pose)以及特征点位置(structure)进行优化。
a) 使用直接法 最小化图像块重投影残差 来获取位姿。 sparse model-based image alignment
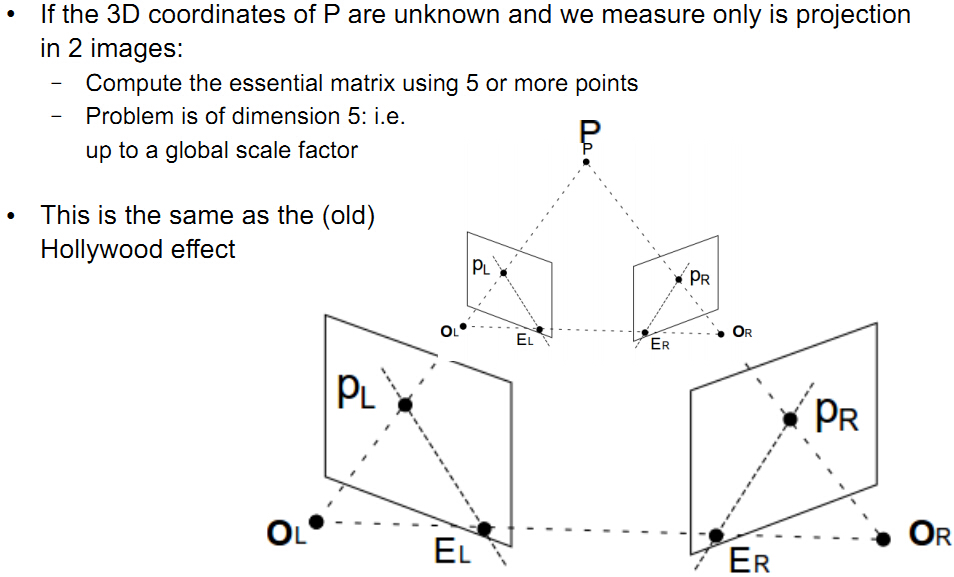
如图所示:其中红色的Tk,k−1为位姿,即优化变量 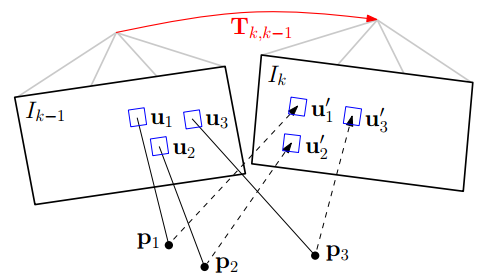
其过程如下,
1. 找到前帧(K-1)看到的地图点p1,p2,p3,对应着2d像素点。
2. 使用变换关系投影至后帧(k)二维图像上,也对应着2d点。
3. 然后最小化灰度误差函数(这是一个最优化过程,又称图像对齐),得到位姿,over。
直接法具体过程如下:
step1. 准备工作。
假设当前相邻帧之间的位姿Tk,k−1的初始值已知,
一般初始化为上一相邻时刻的位姿或者假设为单位矩阵[I,0]。
通过之前多帧之间的特征检测以及深度估计,
我们已经知道 第k-1帧 (参考帧)中 特征点位置 以及 它们的 深度(一般为逆深度)。
step2. 重投影。
获取参考帧3d点:
知道Ik−1中的某个特征点在图像平面的位置(u,v),
以及它的深度dd,能够将该特征投影到三维空间pk−1 = dd * k逆 * (u,v,1),
该三维空间的坐标系是定义在Ik−1摄像机坐标系的。
投影到 当前帧2维像素平面,计算亚像素灰度值:
所以,我们要将它投影到当前帧Ik中,需要位姿转换Tk,k−1=[R, t],
得到该点在当前帧坐标系中的三维坐标pk= T*pk−1 = R*pk−1 + t
最后通过摄像机内参数,投影到Ik的图像平面(u′,v′) = k * pk,
得到的是浮点数坐标,需要根据周围的4个点按照距离加权得到亚像素灰度值。
完成重投影。
step3. 迭代优化更新位姿 。
按理来说对于空间中同一个点,被极短时间内的相邻两帧拍到,它的亮度值应该没啥变化。
使用参考帧特征点(u,v)灰度值 - 投影点(u′,v′) 在当前帧亚像素灰度值 得到误差。
但由于位姿是假设的一个值,所以重投影的点不准确,导致投影前后的亮度值是不相等的。
不断优化位姿使得这个残差最小,就能得到优化后的位姿Tk,k−1。
这里使用 加权LM优化算法得到 位姿Tk,k−1。
将上述过程公式化如下:通过不断优化位姿Tk,k−1Tk,k−1最小化残差损失函数。 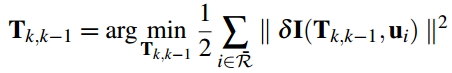
其中,2d->3d->3d->2d 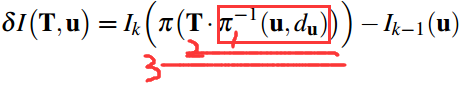
1. 公式中第一步为根据参考帧图像特征点位置和深度逆投影到三维空间,
pk−1 = dd * k逆 * (u,v,1)
2. 第二步将三维坐标点旋转平移到当前帧坐标系下,
pk= T*pk−1 = R*pk−1 + t
3. 第三步再将三维坐标点投影回当前帧图像坐标。
(u′,v′) = k * pk,
这里得到是浮点数坐标,
需要根据周围的4个点按照距离加权得到亚像素灰度值。
当然在优化过程中,残差的计算方式不止这一种形式:
有前向(forwards),
逆向(inverse)之分,
并且还有叠加式(additive)和
构造式(compositional)之分。
这方面可以读读光流法方面的论文,
Baker的大作《Lucas-Kanade 20 Years On: A Unifying Framework》。
选择的方式不同,在迭代优化过程中计算雅克比矩阵的时候就有差别,一般为了减小计算量,
都采用的是inverse compositional algorithm(逆向组成算法)。
上述最小化的误差方程式非凸的,时非线性最小化二乘问题,
可以用高斯牛顿迭代法GN求解,通常会使用期升级版LM列文伯格马尔夸克算法,
再者为了减小外点的影响,会根据投影误差的大小确定误差的权重,使用加权LM算法优化求解。
位姿的迭代增量ξξ(李代数)可以通过下述方程计算:
J转置 * J * se3 = -J * err 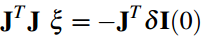
其中雅克比矩阵J 为图像残差对李代数的求导,可以通过链式求导得到: 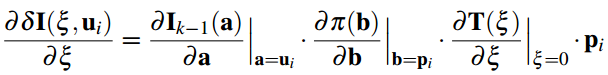
这中间最复杂的部分是位姿矩阵对李代数的求导。
很多文献都有提到过,比如DTAM作者Newcombe的博士论文,
gtsam的作者Dellaert的数学笔记。
不在这里展开(有两篇博客的篇幅),
可以参看清华大学王京的李代数笔记。
到这里,我们已经能够估计位姿了,但是这个位姿肯定不是完美的。
导致重投影预测的特征点在Ik中的位置并不和真正的吻合,也就是还会有残差的存在。
如下图所示: 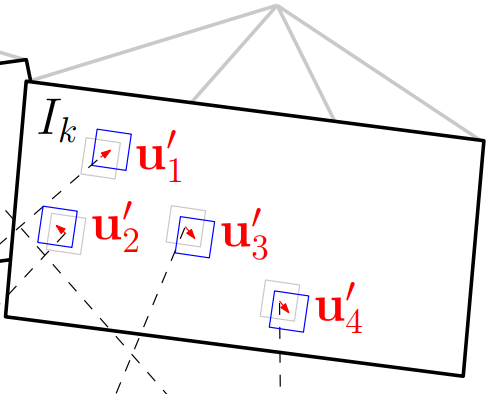
图中灰色的特征块为真实位置,蓝色特征块为预测位置。
幸好,他们偏差不大,可以构造残差目标函数,
和上面直接法类似,不过优化变量不再是相机位姿,
而是像素的位置(u′,v′)(u′,v′),通过迭代对特征块的预测位置进行优化。
这就是svo中提到的Feature Alignment。
最小二乘优化算法简介 L-K算法(或称光流法)本质上是一种基于梯度下降的优化方法。
模板 I 和 T
位置x 变换关系W 变换参数R
误差函数 E = SUM(I(W(x,R)) - T(x))^2
= SUM(I(W(x,R+detR)) - T(x))^2
求解R使得误差函数E最小:
首先 要是E最小,需要使得其导数E'=0可以得到E的局部最小值
对E进行一阶泰勒展开
E= SUM(I(W(x,R)) + E'*detR - T(x))^2
再求导 E'= 2*SUM(E'*(I(W(x,R)) + E'*detR - T(x))) = 0
得到 :
detR = - (E'转置*E')逆 *E'转置* (I(W(x,R)) - T(x))
= - H逆 * J * err , H逆 = (J转置 * J)逆
H* detR = -J * err
这里也可以加入一个权重,根据err的大小计算的一个权重w
H* w* detR = -J * w* err
写成线性方程组形式:
A* detR = b
可使用多种 矩阵分解方法求解该线性方程组,得到 更新变量 detR
se3下的 detR 指数映射到SE3 通过 李群乘法直接 对 变换矩阵R 左乘更新
把H=J转置J叫作Hessian矩阵,它是对J求伪逆过程的一个副产品,和表达二阶偏导的Hessian阵不同。
不过H的作用很重要,它能反映图像数据的统计特性。
如果不幸H是奇异的,也就是说无法求逆矩阵,
那么说明这个图像模板包含的各个梯度方向的信息不足以进行跟踪应用。
J逆 = (J转置*J)逆 * J转置 = J逆 * (J转置)逆 * J转置 = J逆
(J转置*J)逆 * J转置 又称为 伪逆
前向加性算法
I <---- T
T - I(W(Tx, R)) 像素误差
计算 I(W(Tx, R))中各个点在I中的梯度 DetI
T中各个像素点的坐标对应到 ----->I的梯度图像 DetI 中各个点的坐标
逆向组成算法
b) 最小二乘优化特征块的预测位置 更新3d-2d特征块匹配关系 Relaxation Through Feature Alignment
通过第一步的帧间匹配能够得到当前帧相机的位姿,
但是这种frame to frame估计位姿的方式不可避免的会带来累计误差从而导致漂移。
所以,应该通过已经建立好的地图模型,来进一步约束当前帧的位姿。
地图模型通常来说保存的就是三维空间点,
因为每一个Key frame通过深度估计能够得到特征点的三维坐标,
这些三维坐标点通过特征点在Key Frame中进行保存。
所以SVO地图上保存的是Key Frame
以及还未插入地图的KF中的已经收敛的3d点坐标(这些3d点坐标是在世界坐标系下的),
也就是说地图map不需要自己管理所有的3d点,它只需要管理KF就行了。
当新的帧new frame和 相邻关键帧KF的平移量超过场景深度平均值的12%时(比如四轴上升,机器人向前运动),
new frame就会被当做KF,它会被立即插入地图。
同时,又在这个新的KF上检测新的特征点作为深度估计的seed,
这些seed会不断融合新的new frame进行深度估计。
但是,如果有些seed点3d点位姿通过深度估计已经收敛了,怎么办?
map用一个point_candidates来保存这些尚未插入地图中的点。
所以map这个数据结构中保存了两样东西,以前的KF 以及新的尚未插入地图的KF 中已经收敛的3d点。
通过地图我们保存了很多三维空间点,很明显,每一个new frame都是可能看到地图中的某些点的。
由于new frame的位姿通过上一步的直接法已经计算出来了,
按理来说这些被看到的地图上的点可以被投影到这个new frame中,即图中的蓝色方框块。
上图中分析了,所有位姿误差导致这个方框块在new frame中肯定不是真正的特征块所处的位置。
所以需要Feature Alignment来找到地图中特征块在new frame中应该出现的位置,
根据这个位置误差为进一步的优化做准备。
基于光度不变性假设,特征块在以前参考帧中的亮度(灰度值)应该和new frame中的亮度差不多。
所以可以重新构造一个残差,对特征预测位置进行优化。 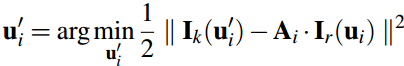
注意这里的优化变量是像素位置,这过程就是 光流法跟踪,
并且注意,
光度误差的前一部分是当前图像中的亮度值 Ik,
后一部分不是前一个参考帧 Ik−1 而是Ir(3d点所在的关键帧),
即它是根据投影的3d点追溯到的这个3d点所在的key frame中的像素值,而不是相邻帧。
由于是特征块对比并且3d点所在的KF可能离当前帧new frame比较远(观察的角度变换了,观察的形状不一样了),
所以光度误差和前面不一样的是还加了一个仿射变换,
需要对KF帧中的特征块进行旋转拉伸之类仿射变换后才能和当前帧的特征块对比。
这时候的迭代量计算方程和之前是一样的,只不过雅克比矩阵变了,这里的雅克比矩阵很好计算:
J=[∂r/∂u′
∂r/∂v′] = [∂I(u′,v′)/∂u′
∂I(u′,v′)/∂v′]
这不就是图像横纵两个方向的梯度嘛.
通过这一步我们能够得到优化后的特征点预测位置,
它比之前通过相机位姿预测的位置更准,
所以反过来,我们利用这个优化后的特征位置,
能够进一步去优化相机位姿以及特征点的三维坐标。
所以位姿估计的最后一步就是Pose and Structure Refinement。
c) 使用优化后的 3d-2d特征块匹配关系, 再次使用直接法, 来对相机位姿(pose)以及特征点位置(structure)进行反向优化。 Pose and Structure Refinement
在一开始的直接法匹配中,我们是使用的光度误差(灰度误差),
这里由于优化后的特征位置 和 之前预测的特征位置存在差异,这个能用来构造新的优化目标函数。
注意上式中误差变成了像素重投影以后位置的差异(不是像素值的差异),
优化变量还是相机位姿(r,p,y,tx,ty,tz),雅克比矩阵大小为2×6(横纵坐标u,v,分别对六个李代数变量求导)。
这一步是就叫做motion-only Bundler Adjustment。
同时根据根据这个误差定义,我们还能够对获取的三维点的坐标(x,y,z)进行优化,
还是上面的像素位置误差形式,
只不过优化变量变成三维点的坐标,这一步叫Structure -only Bundler Adjustment,
优化过程中雅克比矩阵大小为2×3(横纵坐标u,v分别对点坐标(x,y,z)变量求导)。
2. 深度估计 depth估计
最基本的深度估计就是三角化,
这是多视角几何的基础内容(可以参看圣经Hartly的《Multiple View Geometry in Computer Vision》
中的第十二章structure computation.
用单应变换矩阵H或者本质矩阵E 求解得到相邻两帧的变换矩阵R,t后就可是使用类似双目的
三角测距原理来得到深度。
上图中的物理物理中的点 P =[X,Y,Z,1]
在两相机归一化平面下的点 x1 x2 [x,y,z]
在两相机像素平面上的点 p1, p2,匹配点对 [u,v,1]
p1 = k × [R1 t1] × P
左乘 k逆 × p1 = [R1 t1] × P
得到 x1 = T1 × P
计算 x1叉乘x1 = x1叉乘T1 × P = 0
这里 T1 = [I, 0 0 0] 为单位矩阵。
p2 = k × [R2 t2] × P
左乘 k逆 × p2 = [R2 t2] × P
得到 x2 = T2 × P
消去 x2叉乘x2 = x2叉乘T2 × P = 0
式中:
x1 = k逆 × p1 ,
x2 = k逆 × p2 ,
T2= [R, t]为帧1变换到帧2的 已知
得到两个方程
x1叉乘T1 × P = 0
x2叉乘T2 × P = 0
写成矩阵形式 A*P = 0
A = [x1叉乘T1; x2叉乘T2]
这又是一个要用最小二乘求解的线性方程方程组 ,和求本征矩阵一样,
计算矩阵A的SVD分解,然后奇异值最小的那个奇异向量就是三维坐标P的解。
P是3维齐次坐标,需要除以第四个尺度因子 归一化.
[U,D,V] = svd(A);
P = V[:,4] 最后一列
P = P/P(4);// 归一化
以上也是由本质矩阵E = t 叉乘 R 恢复变换矩阵R,t的时候,有四种情况,但是只有一种是正确的。
而判断正确的标准,就是按照这个R,t 计算出来的深度值都是正值,因为相机正前方为Z轴正方向。
我们知道通过两帧图像的匹配点就可以计算出这一点的深度值,
如果有多幅匹配的图像,那就能计算出这一点的多个深度值。
一幅图像对应另外n幅图像,可以看作为n个深度传感器,
把得到点的深度信息的问题看作是有噪声的多传感器数据融合的问题,
使用Gaussian Uniform mixture model(高斯均值混合模型)来对这一问题进行建模,
假设好的测量值符合正态分布,好的测量值的比例为pi,
噪声符合均匀分布,噪声比例为1-pi 使用贝叶斯方法不断更新这个模型,
让点的深度(也就是正态分布中的均值参数)和好的测量值的比例pi收敛到真实值。
这就像对同一个状态变量我们进行了多次测量,
因此,可以用贝叶斯估计来对多个测量值进行融合,
使得估计的不确定性缩小。
如下图所示: 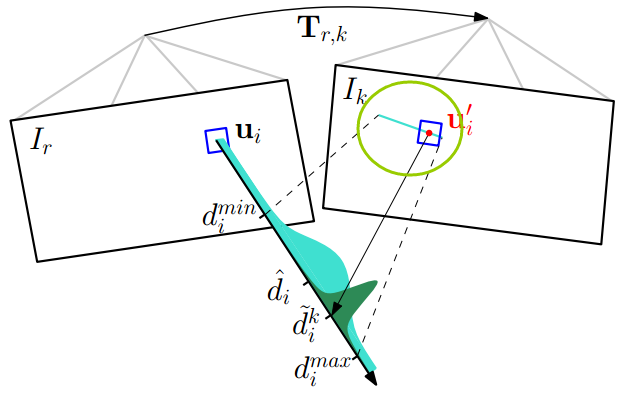
一开始深度估计的不确定性较大(浅绿色部分),
通过三角化得到一个深度估计值以后,
能够极大的缩小这个不确定性(墨绿色部分)。
极线搜索匹配点三角化计算深度 概率方法分析图像点的深度信息
深度估计的思路论文 Video-based, Real-Time Multi View Stereo
在这里,先简单介绍下svo中的三角化计算深度的过程,主要是极线搜索确定匹配点。
在参考帧Ir中,我们知道了一个特征的图像位置ui,假设它的深度值在[dmin,dmax]之间,
那么根据这两个端点深度值,我们能够计算出他们在当前帧Ik中的位置,
如上图中草绿色圆圈中的蓝色线段。
确定了特征出现的极线段位置,就可以进行特征搜索匹配了。
如果极线段很短,小于两个像素,
那直接使用上面求位姿时提到的Feature Alignment光流法就可以比较准确地预测特征位置。
如果极线段很长,那分两步走,第一步在极线段上间隔采样,
对采样的多个特征块一一和参考帧中的特征块匹配,
用Zero mean Sum of Squared Differences (零均值差平方和)方法对各采样特征块评分,
哪个得分最高,说明他和参考帧中的特征块最匹配。
第二步就是在这个得分最高点附近使用Feature Alignment得到次像素精度的特征点位置。
像素点位置确定了,就可以三角化计算深度了。
得到一个新的深度估计值以后,用贝叶斯概率模型对深度值更新。
在LSD slam中,假设深度估计值服从高斯分布,
用卡尔曼滤波(贝叶斯的一种)来更新深度值。
这种假设中,他认为深度估计值效果很棒,
很大的概率出现在真实值(高斯分布均值)附近。
而SVO的作者采用的是Vogiatzis的
论文《Video-based, real-time multi-view stereo》提到的概率模型: 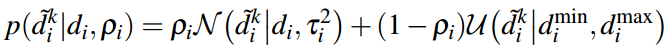
一幅图像中的像素点为中心产生一个patch,
在另一幅图像对应的极线上搜索patch,
使用NCC(NormalizedCrossCorrelation 归一化的交叉相关性)来分析两个patch间的相似程度,
NCC(NormalizedCrossCorrelation 归一化的交叉相关性博客参考
图像总大小M x N,mxn表示带匹配的窗口大小,
这样的计算复杂度就为O(m x n x M x N)。
其中f为其中一幅图像上的窗口
r为另一幅图像上的窗口
ur,uf为对应串口内像素的均值
通过积分图像建立起来窗口下面的待检测图像与模板图像
的和
与平方和
以及他们的交叉乘积
五个积分图索引之后,这样就完成了整个预计算生成。
依靠索引表查找计算结果,
NCC就可以实现线性时间的复杂度计算,
而且时间消耗近似常量跟窗口半径大小无关,
完全可以满足实时对象检测工业环境工作条件。
在深度[X(min),X(max)]区间内进行搜索匹配,求的,
这个区间内NCC的计算结果会产生一系列局部极值。
把上述计算过程看作是一个深度传感器的计算过程,
其输出结果为一系列NCC的局部极值对应的点的深度信息。
它们是有噪声的数据。
这个概率模型是一个 高斯分布 加上一个设定
在最小深度dmin和最大深度dmax之间的 均匀分布。
这个均匀分布的意义是假设会有一定的概率出现错误的深度估计值。
其中pi π 表示x为有效测量(高斯分布)的概率,而(1-pi)为噪声出现错误的概率 
一幅图像对应另外n幅图像,可以看作为n个深度传感器,
把得到点的深度信息的问题看作是有噪声的多传感器数据融合的问题,
使用Gaussian Uniform mixture model
(高斯均匀混合模型,GUMM,另外GMM高斯混合模型)来对这一问题进行建模,
假设好的测量值符合正态分布,
噪声符合均匀分布,
好的测量值的比例为pi,
使用贝叶斯方法不断更新这个模型,
让点的深度(也就是正态分布中的均值参数)和好的测量值的比例pi收敛到真实值。
实际实现的时候一个seed对应与图像中一个像素,这个像素是想要求得其深度信息的点。
一个seed还关联五个参数,
其中四个参数是模型中的参数:
1、好的测量值和
2、坏的测量值的个数,
3、深度估计中高斯分布的均值和
4、方差。
最后一个参数是以这个像素点为中心的一个正方形patch,
计算这个patch和其他图像中的对应极线上的patch的NCC值,
此处因为计算量的关系不会搜索整个极线,只会搜索以目前模型中高斯分布的均值(深度)
对应的极线上的像素点为中心的一个固定范围。
同时,有关这个概率模型递推更新的过程具体可以看Vogiatzis在论文中
提到的Supplementary material,论文中告知了下载地址。
知道了这个贝叶斯概率模型的递推过程,程序就可以实现深度值的融合了,
结合supplementary material去看svo代码中的updateSeeds(frame)这个程序就容易了,
整个程序里的那些参数的计算递归过程的推导,我简单截个图,
这部分我也没细看(公式19是错误的,svo作者指出了),
现在有几篇博客对该部分进行了推导.
每次新进一帧,依照这样的过程:
1. 产生新的seed(seed的数目固定,上次迭代结束时会去掉一些seed)
2. 对每个seed进行更新:
在此帧上进行相关seed的对极搜索;
检测极线上点对应patch与seed中的patch的NCC分数的局部极大值(越大越相似);
用这些局部最大值更新seed中的四个参数。
3. 去掉那些好的测量值的个数低于阈值的,
如果好的测量值的个数高于阈值而且方差低于一个阈值,
把这个seed对应的点的三位坐标算出来并加到地图中。 [svo的Supplementary matterial 推导过程](https://blog.csdn.net/u013004597/article/details/52069741)
SVO深度滤波对深度进行渐进式融合(动态融合)。其过程可表述如下:
关键帧上选取像素点(SVO是fast角点,REMODE是梯度点),
作为种子(seed,种子就是深度未收敛的像素点),
每来一帧图像,融合更新一下之前提取的种子,直至种子的深度收敛,
这是个动态过程,类似于滤波,大概这就是叫深度滤波的原因吧。
如果新的一帧是关键帧,那么再次提取新的像素点作为种子。
就这样旧的种子不断收敛,新的种子不断增加,不断进行下去。
在深度估计的过程中,除了计算深度值外,这个深度值的不确定性(加权值)也是需要计算的,
它在很多地方都会用到,如极线搜索中确定极线的起始位置和长度,
如用贝叶斯概率更新深度的过程中用它来确定更新权重(就像卡尔曼滤波中协方差矩阵扮演的角色),
如判断这个深度点是否收敛了,如果收敛就插入地图等等。
SVO的作者Forster作为第二作者发表的
《REMODE: Probabilistic, Monocular Dense Reconstruction in Real Time》
中对由于特征定位不准导致的三角化深度误差进行了分析,
如下图: 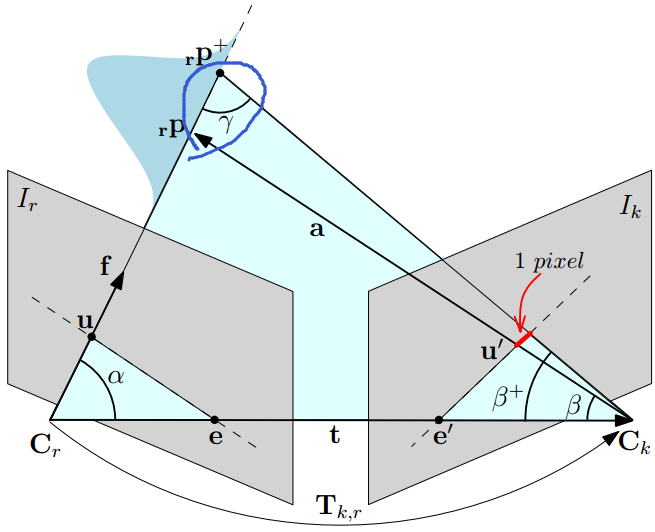
最后,简单说下SVO的初始化过程:
它假设前两个关键帧所拍到的特征点在一个平面上(四轴飞行棋对地面进行拍摄),
1. 然后估计单应性H矩阵,p2 = H * p1 ,恢复R,t矩阵
2. 并通过三角化来估计初始特征点的深度值。
SVO初始化时triangulation的方法具体代码是vikit/math_utils.cpp里的triangulateFeatureNonLin()函数,
使用的是中点法,关于这个三角化代码算法的推导见github issue。
还有就是SVO适用于摄像头垂直向下的情况(也就是无人机上,垂直向上也可以,朝着一面墙也可以),
为什么呢?
1.初始化的时候假设的是平面模型
2.KF的选择是个极大的限制,除了KF的选择原因外摄像头水平朝前运动的时候,
SVO中的深度滤波做的不好,这个讨论可以看看github issue,
然而在我的测试中,不知道修改了哪些参数,稍微改动了部分代码,发现前向运动,
并且对着非平面SVO也是很溜的。 同时我也对svo的代码加了一些中文注释,后续会放到github上,希望帮助大家加快理解svo。最
后,祝大家好运,一起分享知识。
SVO代码
SVO也是将一帧图像处理成多层图像金字塔形式,跟踪过程,也就是通过灰度残差最小来算相机位姿(直接法),
这部分都在FrameHandlerMono类的addImage方法中,addImage方法完成初始化过程和相机位姿跟踪的部分,
跟踪部分中存在四个系统状态:
第一帧关键帧 (处理第一帧到第一个关键帧之间的,fast角点特征匹配,单应变换求取位姿变换),
第二帧关键帧 (光流法金字塔多尺度跟踪上一帧,单应性矩阵求取位姿变换,局部BA优化,深度值滤波器滤波),
其他帧 (上帧位姿初始值,直接法最小化重投影误差优化变换矩阵,匹配点,3d点,深度值滤波器滤波),
重定位模式(relocalizing 跟踪上一帧的参考帧 ),
一二帧是初始化(算单应矩阵分解求位姿),
其他帧就是有了初始地图之后的跟踪过程,具体函数为FrameHandlerMono类的processFrame函数,
这个函数中的跟踪过程与论文中基本一样,
也包括几个步骤:
图像配准(alignment)求位姿,
优化特征点的二维坐标,
同时优化位姿和特征点坐标(BA)。
建图部分的主要函数在depthfilter类中,流程是首先在ros节点调用的时候会调用这个类的startThread函数,
新开线程,线程里运行depthfiler类中的 updateSeedsLoop方法,
大致过程也就是等tracking部分向一个vector或者list中填充它选择的关键帧,
如果有,就进行概率化建图,这个部分还没仔细看。
对应SVO论文中跟踪部分的三个过程,
一是通过当前帧和上一帧的特征点对应的patch之间的灰度残差最小来求当前帧的位姿(即SE(3) T),
一个函数完成,这是一个粗略估计,有了这个粗略估计就可以进行下一步:
把地图中已有的在当前帧可见的特征点重投影到当前帧,一个重投影函数完成,
这个重投影过程完成之后会分析重投影的质量,也就是匹配到的特征点对的个数,
当点对太少的时候就会直接把当前帧的位姿设置为上一帧的位姿,并报错匹配特征点过少,
这也是我常遇到的问题。
最后是优化两个部分:
一是之前粗略估计出的T,这一步叫做 pose优化;
二是投影到当前帧的点在世界坐标系下的坐标点,这一步叫做structure优化。
最后是可选的BA算法同时对位姿和三维点坐标进行优化。
以下分析均在rpg_svo文件夹下:
first:在svo_ros/src中vo_node文件中包含了了节点类vo_node的相关声明,
并包含一个main函数
vo_node.cpp的main中:
1.包含一些ros节点的基本操作,在vo_node的构造函数中,
实例化了一个FrameHandlerMono的对象vo_,并运行vo_->start
2.使用subscribe(cam_topic, 5, &svo::VoNode::imgCb, &vo_node),
每次获得图像时使用VoNode中的imgCb方法处理
3.在imgCb方法中,运行了FrameHandlerMono对象vo_的成员函数addImage,
此方法中其他的部分是关于显示的,即Visualizer类的一些操作。
3.当ros::ok()为真,且vo_node.quit_为假时,循环ros::spinOnce()
----------------------------------------------------------------------------------------------
FrameHandlerMono类继承自FrameHandlerBase类:
1.其构造函数中运行FrameHandlerMono.initialize()
2.initialize()函数中实例化DepthFilter类的一个对象,
运行此对象的startThread()函数,此函数使用boost的thread方法新建了一个线程,
并在此线程中运行DepthFilter.updateSeedsLoop函数。
3.在updateSeedsLoop函数中,
会检查frame_queue_队列中是否有FramePtr存在,
FramePtr在global.h中定义为boost::shared_ptr
==========frame_handler_mono.cpp ================
processFirstFrame(); // 作用是处理第1帧并将其设置为关键帧;
processSecondFrame();// 作用是处理第1帧后面所有帧,直至找到一个新的关键帧;
processFrame(); // 作用是处理两个关键帧之后的所有帧;
relocalizeFrame(=); //作用是在相关位置重定位帧以提供关键帧
startFrameProcessingCommon(timestamp) 设置处理第一帧 stage_ = STAGE_FIRST_FRAME;
processFirstFrame(); 处理第一帧,直到找打第一个关键帧==============================================
1. fast角点特征,单应变换求取位姿变换,特点点数超过100个点才设置第一帧为为关键帧,
2. 计算单应性矩阵(根据前两个关键帧)来初始化位姿,3d点
3. 且设置系统处理标志为第二帧 stage_ = STAGE_SECOND_FRAME
processSecondFrame(); 处理第一帧关键帧到第二帧关键帧之间的所有帧(跟踪上一帧) ========================
1. 光流法 金字塔多尺度 跟踪关键点,根据跟踪的数量和阈值,做跟踪成功/失败的判断
2. 前后两帧计算单应性矩阵,根据重投影误差记录内点数量,根据阈值,判断跟踪 成功/失败,计算3d点
3. 集束调整优化, 非线性最小二乘优化,
4. 计算场景深度均值和最小值
5. 深度滤波器对深度进行滤波,高斯均值混合模型进行更新深度值
6. 设置系统状态 stage_= STAGE_DEFAULT_FRAME;
processFrame(); 处理前两个关键帧后的所有帧(跟踪上一帧) ============================================
1. 设置初始位姿, 上帧的位姿初始化为当前帧的位姿
2. 直接法 最小化 3d-2d 重投影 像素误差 求解位姿 LM算法优化位姿)
3. 最小化 3d-2d 重投影像素误差 优化特征块的预测位置 更新3d-2d特征块匹配关系
4. 使用优化后的 3d-2d特征块匹配关系, 类似直接法,最小化2d位置误差,来优化相机位姿(pose)
5. 使用优化后的 3d-2d特征块匹配关系, 类似直接法,最小化2d位置误差,来优化3D点(structure)
6. 深度值滤波
relocalizeFrame(); 重定位模式(跟踪参考帧)=======================================================
1. 得到上一帧附近的关键帧作为参考帧 ref_keyframe
2. 进行直接法 最小化 3d-2d 重投影 像素误差 求解当前帧的位姿
3. 若跟踪质量较高(匹配特征点数大于30) 将参考帧设置为上一帧
4. 直接法跟踪上一帧参考帧进行processFrame()处理( 其实就是跟踪参考帧模式 )
5. 如果跟踪成功就设置为相应的跟踪后的位姿,否者设置为参考帧的位姿
项目代码结构
rpg_svo
├── rqt_svo 为与 显示界面 有关的功能插件
├── svo 主程序文件,编译 svo_ros 时需要
│ ├── include
│ │ └── svo
│ │ ├── bundle_adjustment.h 光束法平差(图优化)
│ │ ├── config.h SVO的全局配置
│ │ ├── depth_filter.h 像素深度估计(基于概率) 高斯均值混合模型
│ │ ├── feature_alignment.h 特征匹配
│ │ ├── feature_detection.h 特征检测 faster角点
│ │ ├── feature.h(无对应cpp) 特征定义
│ │ ├── frame.h frame定义
│ │ ├── frame_handler_base.h 视觉前端基础类
│ │ ├── frame_handler_mono.h 单目视觉前端原理(较重要)==============================
│ │ ├── global.h(无对应cpp) 有关全局的一些配置
│ │ ├── initialization.h 单目初始化
│ │ ├── map.h 地图的生成与管理
│ │ ├── matcher.h 重投影匹配与极线搜索
│ │ ├── point.h 3D点的定义
│ │ ├── pose_optimizer.h 图优化(光束法平差最优化重投影误差)
│ │ ├── reprojector.h 重投影
│ │ └── sparse_img_align.h 直接法优化位姿(最小化光度误差)
│ ├── src
│ │ ├── bundle_adjustment.cpp
│ │ ├── config.cpp
│ │ ├── depth_filter.cpp
│ │ ├── feature_alignment.cpp
│ │ ├── feature_detection.cpp
│ │ ├── frame.cpp
│ │ ├── frame_handler_base.cpp
│ │ ├── frame_handler_mono.cpp
│ │ ├── initialization.cpp
│ │ ├── map.cpp
│ │ ├── matcher.cpp
│ │ ├── point.cpp
│ │ ├── pose_optimizer.cpp
│ │ ├── reprojector.cpp
│ │ └── sparse_img_align.cpp
├── svo_analysis 未知
├── svo_msgs 一些配置文件,编译 svo_ros 时需要
└── svo_ros 为与ros有关的程序,包括 launch 文件
├── CMakeLists.txt 定义ROS节点并指导rpg_svo的编译
├── include
│ └── svo_ros
│ └── visualizer.h
├── launch
│ └── test_rig3.launch ROS启动文件
├── package.xml
├── param 摄像头等一些配置文件
├── rviz_config.rviz Rviz配置文件(启动Rviz时调用)
└── src
├── benchmark_node.cpp
├── visualizer.cpp 地图可视化
└── vo_node.cpp VO主节点=======================================
转载请注明原地址,万有文的博客:ewenwan.github.io 谢谢!