性能提升方法
1. 小模型 mobilenet , 更精细模型的设计,紧致网络设计
mobilenet squeezenet shufflenet
2. 模型压缩:参数稀疏、剪裁、量化、分解
本部分 [量化](https://github.com/Ewenwan/MVision/blob/master/CNN/Deep_Compression/quantization/readme.md)
3. 软件优化-高性能计算
腾讯 ncnn 小米mace 百度MDL Google TensorFlow Lite
4. 硬件优化-AI芯片
TPU
FPGA上的应用
赛灵思Xilinx
暂时未涉及 [利用 赛灵思Xilinx 器件的INT8优化开展深度学习](https://china.xilinx.com/support/documentation/white_papers/c_wp486-deep-learning-int8.pdf)
Binarized Neural Network TF training code + C matrix / eval library 量化网络框架
Model Compression and Model Acceleration in TensorLayer
如果想把参数压缩方案和其他一些方案结合,
比如上面提到的一些 SqueezeNet,MobileNets,ShuffleNet 结合起来,会对准确率造成比较大的影响。
原因可以归为参数压缩算法其实是一个找次优解的问题,当网络冗余度越小,解越不好找。
所以,目前的高精度压缩算法只适合于传统的有很多冗余的网络。
AI芯片
Efficient Processing of Deep Neural Networks: A Tutorial and Survey
由于目前基于 PC 平台的神经网络加速一定程度上不能满足需要,
开发基于硬件例如 FPGA 的硬件加速平台显得很有必要。
其实硬件加速神经网络前向运算的最主要的任务就是完成卷积优化,
减少卷积运算的资源和能源消耗非常核心。
卷积优化的主要思路
1. 内存换取时间:
如果深度学习中每一层的卷积都是针对同一张图片,
那么所有的卷积核可以一起对这张图片进行卷积运算,
然后再分别存储到不同的位置,这就可以增加内存的使用率,
一次加载图片,产生多次的数据,而不需要多次访问图片,
这就是用内存来换时间。 ### 2. 乘法优化:
以下图为例,上面是两张图片,右边是卷积核。
我们可以把卷积核心展开成一条行,然后多个卷积核就可以排列成多行,
再把图像也用类似的方法展开,就可以把一个卷积问题转换成乘法问题。
这样就是一行乘以一列,就是一个结果了。
这样虽然多做了一些展开的操作,
但是对于计算来讲,速度会提升很多。
3. GPU优化:
1. 了解 IO 访问的情况以及 IO 的性能;
2. 多线程的并行计算特性;
3. IO 和并行计算间的计算时间重叠。
对于 NVIDIA 的 GPU 来讲,内存访问是有一些特性的,
连续合并访问可以很好地利用硬件的带宽。
你可以看到,NVIDIA 最新架构的 GPU,其核心数目可能并没有明显增加,
架构似乎也没有太大变化,但在几个计算流处理器中间增加缓存,
就提高了很大的性能,为 IO 访问这块儿带来了很大优化。 ### 4. 卷积计算优化
目前,卷积的计算大多采用间接计算的方式,主要有以下三种实现方式:
1、im2col + GEMM。
caffe等很多框架中都使用了这种计算方式,
原因是将问题转化为矩阵乘法后可以方便的使用很多矩阵运算库(如MKL、openblas、Eigen等)。
2、FFT变换。
时域卷积等于频域相乘,因此可将问题转化为简单的乘法问题。
3、Winograd。
这种不太熟悉,据说在GPU上效率更高。
NNPACK就是FFT和Winograd方法的结合。
上面三种方法执行效率都还不错,但对内存占用比较高,因为需要存储中间结果或者临时辅助变量。
1、Strassen 算法:
分析 CNN 的线性代数特性,增加加法减少乘法,
这样降低了卷积运算的计算的复杂度(o(n^3) -> o(n^2.81)),
但是这种方法不适合在硬件里面使用,这里就不做详细的介绍了。
2、 MEC:
一种内存利用率高且速度较快的卷积计算方法 [MEC: Memory-efficient Convolution for Deep Neural Network 论文](http://cn.arxiv.org/pdf/1706.06873v1)
5. 卷积中的数据重用
在软件中的卷积运算,其实我们是在不断的读取数据,进行数据计算。
也就是说卷积操作中数据的存取其实是一个很大的浪费,
卷积操作中数据的重用如下图所示.
那么想办法减少数据的重用,减少数据的存取成为解决卷积计算问题的一个很重要的方面。
目前这样的方法有很多种,最主要的方法包括以下几种:
权重固定:最小化权重读取的消耗,最大化卷积和卷积核权重的重复使用;
输出固定:最小化部分和 R/W 能量消耗,最大化本地积累;
NLR (No Local Reuse):使用大型全局缓冲区共享存储,减少 DRAM 访问能耗;
RS:在内部的寄存器中最大化重用和累加,针对整体能源效率进行优化,而不是只针对某种数据类型。
下表是在 45NM CMOS 的基础上对于不同的操作的能耗进行的统计。
对 32 位的各种操作的能耗进行统计,可以看到从 DRAM 里面存取数据的能量消耗是最大的。
是 32 位整型数据进行加法的能量消耗的 6400 倍。
那么,从数据存取角度考虑卷积的优化就显得尤为必要了。
可行性分析
在 GPU 中加速时,主要通过将数据最大程度的并行运算,
增加了 GPU 的使用率从而加快了速度。
但是这种方法在硬件实现的时候是不可行的,因为这种方法本质上没有降低能耗,
而 DNN 模型的高能耗和大量的数据是其在可穿戴设备上面进行部署所需要面对的困难。
下面对一个卷积部分和运算进行分析,如下图 :
对第一组的 PE 整列,输入的是从 Image 的第 0 行到第 R-1 行的 S 列的数据,
同样的对于第二列的 PE 阵列输入的是第 2 行到第 R 的 S 列的数据。
每一列的 PE 计算得到一个最终的 Psum 的结果,那么如果设置 PE 阵列的列数为 N 的话,
每次我们就可以计算得到连续的 N 个部分和的结果。
不断更新 PE(process element,即处理单元)中 Image 缓冲区的数据,
就可以模拟卷积在水平方向上面的滑动,不断更新整个 PE 阵列的数据输入,
就可以模拟卷积窗在垂直方向上面的滑动,最终完成整个卷积运算的实现。
对应的卷积运算公式的细节在图中已经给出了,每一组 PE 产生一个部分和的结果的话,
那么增加 PE 阵列的组数,就可以一次性产生多个部分和计算结果,这里的组数就是并行度。
上面的内容简单论证用数据重用的方式实现卷积运算的可行性,
至于实现的具体数据流,还有相对用的系统的架构。
压缩算法在实际硬件芯片的应用
其实压缩算法应用硬件芯片非常简单,就是简单的将硬件芯片原来使用的乘法器进行替换,
如果是 BNN,参数只有两种情形,
那么如果参数为 1 的时候,直接通过,
不计算,如果参数为 -1 的时候,翻转最高位即可。
同理三值化中增加了一个 0 参数,这个可以直接跳过不进行计算。
至于参数为(-2,-1,0,1,2)的情形,参数为 2 时就增加了一个移位运算,
参数为 -2 的时候增加了一个最高位的翻转。
如果是 DoReFaNet,权值和输出都固定在一定的种类内部,那么他们的乘积情形也只有一定的种类,
这个时候相当于把乘法器变成了一个寻址操作,
每次乘法只需要在 LUT(look-up table,查找表)里面寻找到正确的结果读出即可。
模型压缩
| [超全总结:神经网络加速之量化模型 | 附带代码](https://yq.aliyun.com/articles/598953) |
量化模型(Quantized Model)是一种模型加速(Model Acceleration)方法的总称,
包括二值化网络(Binary Network)、
三值化网络(Ternary Network)、
深度压缩(Deep Compression)、
多比例量化等
为什么要压缩网络?
做过深度学习的应该都知道,NN大法确实效果很赞,
在各个领域轻松碾压传统算法,
不过真正用到实际项目中却会有很大的问题:
计算量非常巨大;
模型特别吃内存;
这两个原因,使得很难把NN大法应用到嵌入式系统中去,
因为嵌入式系统资源有限,而NN模型动不动就好几百兆。
所以,计算量和内存的问题是作者的motivation;
如何压缩?
论文题目已经一句话概括了:
Prunes the network:只保留一些重要的连接;
Quantize the weights:通过权值量化来共享一些weights;
Huffman coding:通过霍夫曼编码进一步压缩;
效果如何?
Pruning:把连接数减少到原来的 1/13~1/9;
Quantization:每一个连接从原来的 32bits 减少到 5bits;
最终效果:
- 把AlextNet压缩了35倍,从 240MB,减小到 6.9MB;
- 把VGG-16压缩了49北,从 552MB 减小到 11.3MB;
- 计算速度是原来的3~4倍,能源消耗是原来的3~7倍;
网络压缩(network compression)
尽管深度神经网络取得了优异的性能,
但巨大的计算和存储开销成为其部署在实际应用中的挑战。
有研究表明,神经网络中的参数存在大量的冗余。
因此,有许多工作致力于在保证准确率的同时降低网路复杂度。 ### 0、训练时对参数的更新进行限制,使其趋向于稀疏.
核参数稀疏: 是在训练过程中,对参数的更新进行限制,使其趋向于稀疏.
对于稀疏矩阵,可以使用更加紧致的存储方式,如CSC,
但是使用稀疏矩阵操作在硬件平台上运算效率不高,
容易受到带宽的影响,因此加速并不明显。
在训练过程中,对权重的更新加以正则项进行诱导,使其更加稀疏,使大部分的权值都为0。
http://papers.nips.cc/paper/6504-learning-structured-sparsity-in-deep-neural-networks.pdf
动态的模型裁剪方法
https://arxiv.org/pdf/1608.04493.pdf
包括以下两个过程:pruning和splicing,其中pruning就是将认为不中要的weight裁掉,
但是往往无法直观的判断哪些weight是否重要,
因此在这里增加了一个splicing的过程,
将哪些重要的被裁掉的weight再恢复回来,
类似于一种外科手术的过程,将重要的结构修补回来。
作者通过在W上增加一个T来实现,T为一个2值矩阵,起到的相当于一个mask的功能,
当某个位置为1时,将该位置的weight保留,为0时,裁剪。
在训练过程中通过一个可学习mask将weight中真正不重要的值剔除,从而使得weight变稀疏。
特点:
核的稀疏化可能需要一些稀疏计算库的支持,其加速的效果可能受到带宽、稀疏度等很多因素的制约;
1、低秩近似 (低秩分解 Low Rank Expansion)
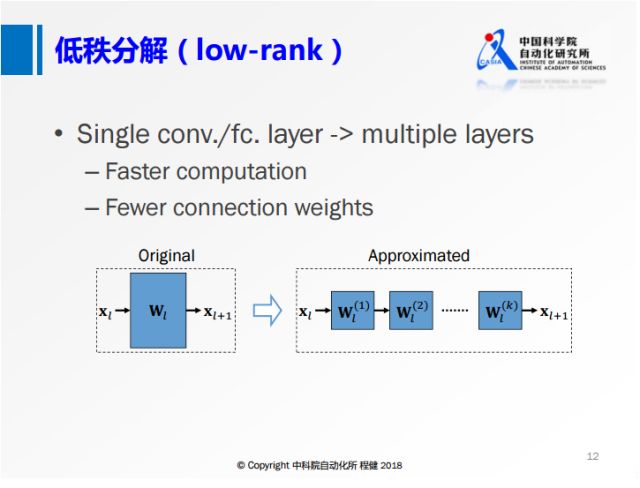
上图展示了低秩分解的基本思想:
将原来大的权重矩阵分解成多个小的矩阵,
右边的小矩阵的计算量都比原来大矩阵的计算量要小,
这是低秩分解的基本出发点。
奇异值分解SVD、CP分解、Tucker分解、Tensor Train分解和Block Term分解
用低秩矩阵近似原有权重矩阵。
例如,可以用SVD得到原矩阵的最优低秩近似,
或用Toeplitz矩阵配合Krylov分解近似原矩阵。
SVD分解:
全连接层的权重矩阵记作 W∈Rm×n ,首先对 W 进行 SVD 分解,如下:
W=USV转置
为了能够用两个较小的矩阵来表示 W ,我们可以取奇异值的前 K 个分量。
于是,W可以通过下式重建:
W^=U^S^V^T,其中U^∈Rm×kV^∈Rn×k
我们唯一需要保存的就是3个比较小的矩阵 U,S,V ,我们可以简单算一下压缩比为 mn/k(m+n+1)
矩阵的秩概念上就是线性独立的纵列(或者横列)的最大数目。
行秩和列秩在线性代数中可以证明是相等的,例如:
3*3的矩阵如下,则 行秩==列秩==秩==3
1 2 3
4 5 6
7 8 9
1*3的矩阵如下,则 行秩==列址==秩==1
[1 2 3]
3*1的矩阵如下,则 行秩==列址==秩==1
[1] [2] [3]
低秩分解,这个名字虽然唬人,
实际上就是把较大的卷积核分解为两个级联的行卷积核和列卷积核。
常见的就是一个3*3的卷积层,替换为一个3*1的卷积层加上一个1*3的卷积核。
容易计算得,
一个特征图10*10,经过3*3卷积核后得到8*8的特征图输出,
而替换为低秩后,
则先得到10*8的特征图然后再得到8*8的特征图。
另外现在越来越多网络中采用1×1的卷积,
而这种小的卷积使用矩阵分解的方法很难实现网络加速和压缩。 #### a、奇异值分解svd 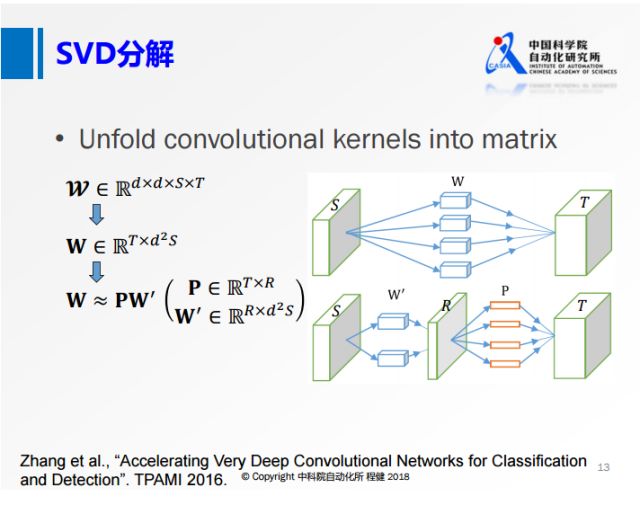
上图是微软在2016年的工作,将卷积核矩阵先做成一个二维的矩阵,再做SVD分解。
上图右侧相当于用一个R的卷积核做卷积,再对R的特征映射做深入的操作。
从上面可以看到,虽然这个R的秩非常小,但是输入的通道S还是非常大的。
b、Tucker分解 解决SVD分解中输入的通道S大的问题
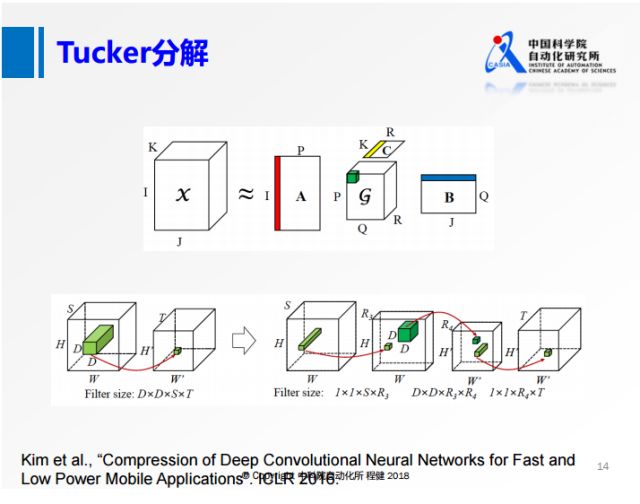
为了解决SVD分解过程中通道S比较大的问题,
我们从另一个角度出发,沿着输入的方向对S做降维操作,这就是上图展示的Tucker分解的思想。
具体操作过程是:
原来的卷积,首先在S维度上做一个低维的表达,
再做一个正常的3×3的卷积,
最后再做一个升维的操作。 #### c、CP分解加速神经网络的方法 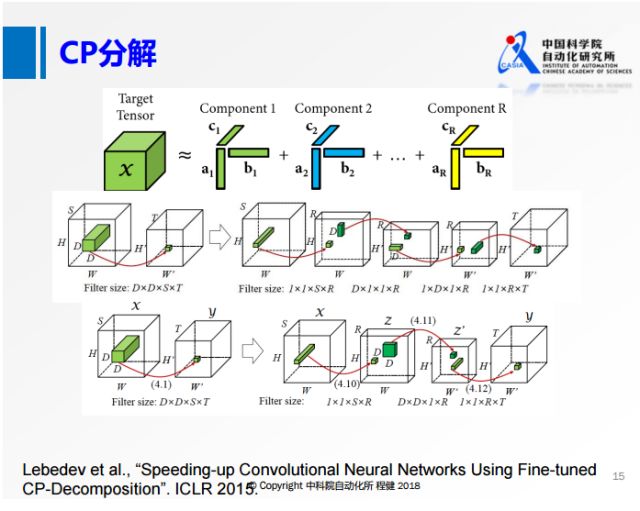
在SVD分解和Tucker分解之后的一些工作主要是做了更进一步的分解。
上图展示了使用微调的CP分解加速神经网络的方法。
在原来的四维张量上,在每个维度上都做类似1×1的卷积,转
化为第二行的形式,在每一个维度上都用很小的卷积核去做卷积。
在空间维度上,大部分都是3×3的卷积,所以空间的维度很小,可以转化成第三行的形式,
在输入和输出通道上做低维分解,但是在空间维度上不做分解,类似于MobileNet。
d、块分解
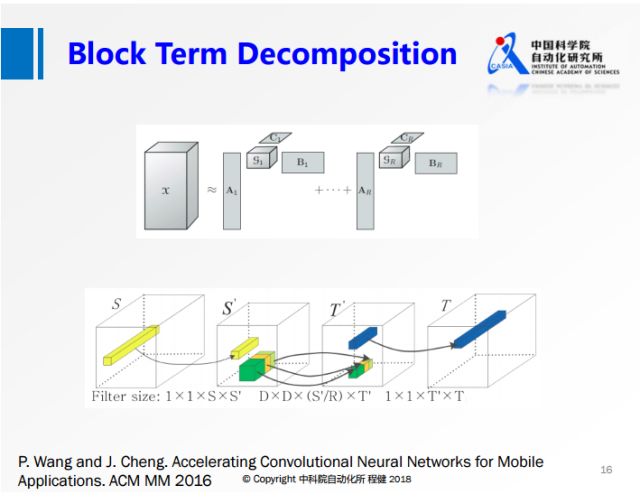
结合了上述两种分解方法各自的优势。首先把输入参数做降维,
然后在第二个卷积的时候,做分组操作,这样可以降低第二个3×3卷积的计算量,最后再做升维操作。
另一方面由于分组是分块卷积,它是有结构的稀疏,所以在实际中可以达到非常高的加速,
我们使用VGG网络在手机上的实验可以达到5-6倍的实际加速效果。
LBCNN 局部二值卷积 卷积稀疏滤波器
2、剪枝(pruning) 在训练结束后,可以将一些不重要的神经元连接
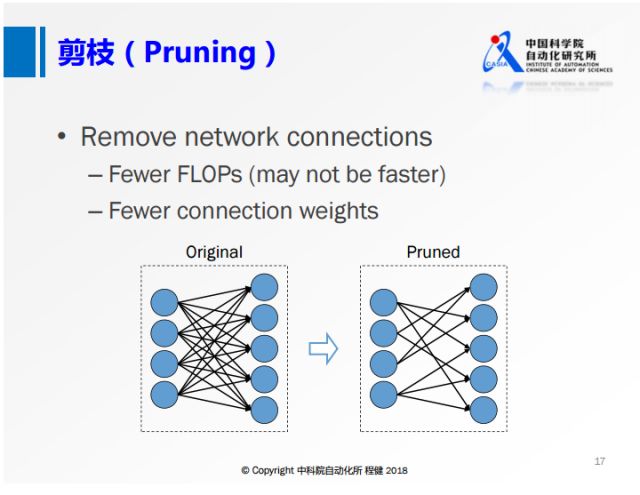
非结构化剪枝Pruning,结构化剪枝Filter Pruning,梯度Pruning等方法
(可用权重数值大小衡量配合损失函数中的稀疏约束)或整个滤波器去除,
之后进行若干轮微调。实际运行中,神经元连接级别的剪枝会
使结果变得稀疏,
不利于缓存优化和内存访问,有的需要专门设计配套的运行库。
相比之下,滤波器级别的剪枝可直接运行在现有的运行库下,
而滤波器级别的剪枝的关键是如何衡量滤波器的重要程度。
例如,可用卷积结果的稀疏程度、该滤波器对损失函数的影响、
或卷积结果对下一层结果的影响来衡量。
特别地,由于计算稀疏矩阵在CPU和GPU上都有特定的方法,所以前向计算也需要对一些部分进行代码修改。
GPU上计算稀疏需要调用cuSPARSE库,
而CPU上计算稀疏需要mkl_sparse之类的库去优化稀疏矩阵的计算,
否则达不到加速效果.
剪枝方法基本流程如下:
1. 正常流程训练一个神经网络。以CAFFE为例,就是普普通通地训练出一个caffemodel。
2. 确定一个需要剪枝的层,一般为全连接层,设定一个裁剪阈值或者比例。
实现上,通过修改代码加入一个与参数矩阵尺寸一致的mask矩阵。
mask矩阵中只有0和1,实际上是用于重新训练的网络。
3. 重新训练微调,参数在计算的时候先乘以该mask,则mask位为1的参数值将继续训练通过BP调整,
而mask位为0的部分因为输出始终为0则不对后续部分产生影响。
4. 输出模型参数储存的时候,因为有大量的稀疏,所以需要重新定义储存的数据结构,
仅储存非零值以及其矩阵位置。重新读取模型参数的时候,就可以还原矩阵。 #### a、非结构化剪枝 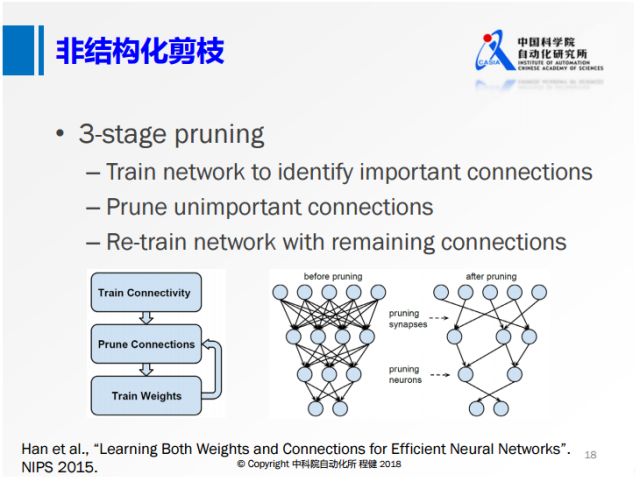
上图展示了在NIP2015上提出的非常经典的三阶段剪枝的方法。
首先训练一个全精度网络,
随后删除一些不重要的节点,
后面再去训练权重。
这种非结构化的剪枝的方法,虽然它的理论计算量可以压缩到很低,
但是收益是非常低的,比如在现在的CPU或者GPU框架下很难达到非常高的加速效果。
所以下面这种结构化的剪枝技术越来越多。 #### b、结构化剪枝 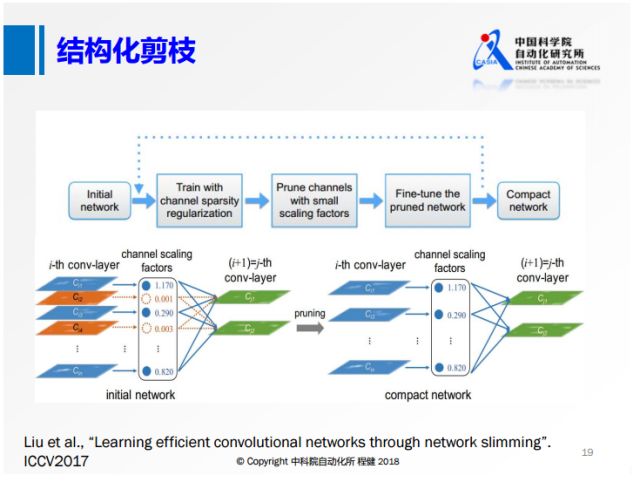
从去年的ICCV就有大量基于channel sparsity的工作。
上面是其中的一个示意图,相当于对每一个feature map定义其重要性,
把不重要的给删除掉,这样产生的稀疏就是有规则的,
我们可以达到非常高的实际加速效果。
3、量化(quantization)。对权重数值进行聚类,
量化的思想非常简单。
CNN参数中数值分布在参数空间,
通过一定的划分方法,
总是可以划分称为k个类别。
然后通过储存这k个类别的中心值或者映射值从而压缩网络的储存。
量化可以分为
Low-Bit Quantization(低比特量化)、
Quantization for General Training Acceleration(总体训练加速量化)和
Gradient Quantization for Distributed Training(分布式训练梯度量化)。
由于在量化、特别是低比特量化实现过程中,
由于量化函数的不连续性,在计算梯度的时候会产生一定的困难。
对此,阿里巴巴冷聪等人把低比特量化转化成ADMM可优化的目标函数,从而由ADMM来优化。
从另一个角度思考这个问题,使用哈希把二值权重量化,再通过哈希求解.
用聚类中心数值代替原权重数值,配合Huffman编码,
具体可包括标量量化或乘积量化。
但如果只考虑权重自身,容易造成量化误差很低,
但分类误差很高的情况。
因此,Quantized CNN优化目标是重构误差最小化。
此外,可以利用哈希进行编码,
即被映射到同一个哈希桶中的权重共享同一个参数值。
聚类例子:
例如下面这个矩阵。
1.2 1.3 6.1
0.9 0.7 6.9
-1.0 -0.9 1.0
设定类别数k=3,通过kmeans聚类。得到:
A类中心: 1.0 , 映射下标: 1
B类中心: 6.5 , 映射下标: 2
C类中心: -0.95 , 映射下标: 3
所以储存矩阵可以变换为(距离哪个中心近,就用中心的下标替换):
1 1 2
1 1 2
3 3 1
当然,论文还提出需要对量化后的值进行重训练,挽回一点丢失的识别率
基本上所有压缩方法都有损,所以重训练还是比较必要的。
Huffman编码笔者已经不太记得了,好像就是高频值用更少的字符储存,低频则用更多。
4、降低数据数值范围。 其实也可以算作量化
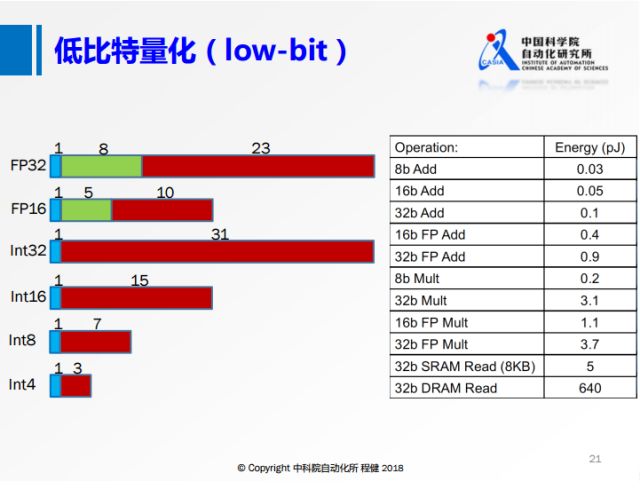
默认情况下数据是单精度浮点数,占32位。
有研究发现,
改用半精度浮点数(16位)几乎不会影响性能。
谷歌TPU使用8位整型来表示数据。
极端情况是数值范围为 二值(0/1) 或 三值 (-1/0/1),
这样仅用位运算即可快速完成所有计算,
但如何对二值或三值网络进行训练是一个关键。
通常做法是网络前馈过程为二值 或 三值,
梯度更新过程为实数值。
5、迁移学习 Knowledge Distillation
在Knowledge Distillation中有两个关键的问题,
一是如何定义知识,
二是使用什么损失函数来度量student网络和teacher 网络之间的相似度。
通过训练一个更大的神经网络模型,再逐步剪枝得到的小模型取得的结果要比直接训练这样一个小模型的结果好得多。
已训练好的模型上做裁剪
这种就是在训练好的模型上做一些修改,
然后在fine-tuning到原来的准确率,
主要有一些方法:
1、剪枝:神经网络是由一层一层的节点通过边连接,每个边上会有权重,
所谓剪枝,就是当我们发现某些边上的权重很小,
可以认为这样的边不重要,进而可以去掉这些边。
在训练的过程中,在训练完大模型之后,
看看哪些边的权值比较小,把这些边去掉,然后继续训练模型;
2、权值共享:就是让一些边共用一个权值,达到缩减参数个数的目的。
假设相邻两层之间是全连接,每层有1000个节点,
那么这两层之间就有1000*1000=100万个权重参数。
可以将这一百万个权值做聚类,利用每一类的均值代替这一类中的每个权值大小,
这样同属于一类的很多边共享相同的权值,假设把一百万个权值聚成一千类,则可以把参数个数从一百万降到一千个。
3、量化:一般而言,神经网络模型的参数都是用的32bit长度的浮点型数表示,
实际上不需要保留那么高的精度,可以通过量化,
比如用0~255表示原来32个bit所表示的精度,
通过牺牲精度来降低每一个权值所需要占用的空间。
4、神经网络二值化:比量化更为极致的做法就是神经网络二值化,
也即将所有的权值不用浮点数表示了,
用二进制的数表示,要么是+1,要么是-1,用二进制的方式表示,
原来一个32bit权值现在只需要一个bit就可以表示,
可以大大减小模型尺寸。
Deep Compression 方法,包含
裁剪,
量化,
编码 三个手段。
模型参数分析:
网络中全连层参数和卷积层weight占绝大多数,
卷积层的bias只占极小部分。
而参数分布在0附近,近似高斯分布。
参数压缩针对卷积层的weight和全连层参数。每一层的参数单独压缩。
1. 剪枝(pruning)
模型的裁剪方法则比较简单明了,直接在原有的模型上剔除掉不重要的filter,
虽然这种压缩方式比较粗糙,但是神经网络的自适应能力很强,
加上大的模型往往冗余比较多,将一些参数剔除之后,
通过一些retraining的手段可以将由剔除参数而降低的性能恢复回来,
因此只需要挑选一种合适的裁剪手段以及retraining方式,
就能够有效的在已有模型的基础上对其进行很大程度的压缩,是目前使用最普遍的方法。
基于模型裁剪的方法:
对以训练好的模型进行裁剪的方法,是目前模型压缩中使用最多的方法,
通常是寻找一种有效的评判手段,来判断参数的重要性,
将不重要的connection或者filter进行裁剪来减少模型的冗余。
a. 阈值剪裁 基于模型裁剪的方法
pruning可以分为三步:
step1. 正常训练模型得到网络权值;
step2. 将所有低于一定阈值的权值设为0;
step3. 重新训练网络中剩下的非零权值。
截止滤波后的稀疏矩阵: 
0很多,直接存储矩阵太浪费,采用CSR 存储方式
记录非零值 以及非零值的 索引,
CSR可以将原始矩阵表达为三部分,即AA,JA,IC 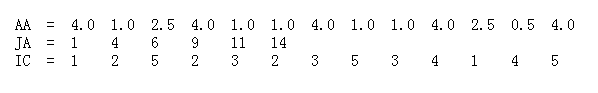
AA是矩阵A中所有非零元素,长度为a,即非零元素个数;
JA是矩阵A中每行第一个非零元素在AA中的位置,最后一个元素是非零元素数加1,长度为n+1, n是矩阵A的行数;
IC是AA中每个元素对应的列号,长度为a。
所以将一个稀疏矩阵转为CSR表示,需要的空间为2*a+n+1个,同理CSC也是类似。
b.基于量级的裁剪方式 相关论文
基于量级的裁剪方式,用weight值的大小来评判其重要性,
对于一个filter,其中所有weight的绝对值求和,后通过排序来区分重要性。
来作为该filter的评价指标,
将一层中值低的filter裁掉,
可以有效的降低模型的复杂度并且不会给模型的性能带来很大的损失.
https://arxiv.org/pdf/1608.08710.pdf
作者在裁剪的时候同样会考虑每一层对裁剪的敏感程度,作者会单独裁剪每一层来看裁剪后的准确率。
对于裁剪较敏感的层,作者使用更小的裁剪力度,或者跳过这些层不进行裁剪。
目前这种方法是实现起来较为简单的,并且也是非常有效的,
它的思路非常简单,就是认为参数越小则越不重要。
c.统计filter中激活为0的值的数量作为标准 论文参考
作者认为,在大型的深度学习网络中,大部分的神经元的激活都是趋向于零的,
而这些激活为0的神经元是冗余的,将它们剔除可以大大降低模型的大小和运算量,
而不会对模型的性能造成影响,于是作者定义了一个量APoZ(Average Percentage of Zeros)
来衡量每一个filter中激活为0的值的数量,来作为评价一个filter是否重要的标准。
d.基于熵值的剪裁 论文参考
作者认为通过weight值的大小很难判定filter的重要性,
通过这个来裁剪的话有可能裁掉一些有用的filter。
因此作者提出了一种基于熵值的裁剪方式,利用熵值来判定filter的重要性。
作者将每一层的输出通过一个Global average Pooling,
将feature map 转换为一个长度为c(filter数量)的向量,
对于n张图像可以得到一个n*c的矩阵,
对于每一个filter,将它分为m个bin,统计每个bin的概率pi,
然后计算它的熵值,利用熵值来判定filter的重要性,再对不重要的filter进行裁剪。
第j个feature map熵值的计算方式如下:
Hj = -sum(pi*log(pi))
在retrain中,作者使用了这样的策略,即每裁剪完一层,通过少数几个迭代来恢复部分的性能,
当所有层都裁剪完之后,再通过较多的迭代来恢复整体的性能,
作者提出,在每一层裁剪过后只使用很少的训练步骤来恢复性能,
能够有效的避免模型进入到局部最优。
e.基于能量效率的裁剪方式 论文参考
作者认为以往的裁剪方法,都没有考虑到模型的带宽以及能量的消耗,
因此无法从能量利用率上最大限度的裁剪模型,因此提出了一种基于能量效率的裁剪方式。
作者指出一个模型中的能量消耗包含两个部分,一部分是计算的能耗,一部分是数据转移的能耗,
在作者之前的一片论文中(与NVIDIA合作,Eyeriss),提出了一种估计硬件能耗的工具,
能够对模型的每一层计算它们的能量消耗。然后将每一层的能量消耗从大到小排序,
对能耗大的层优先进行裁剪,这样能够最大限度的降低模型的能耗,对于需要裁剪的层,
根据weight的大小来选择不重要的进行裁剪,同样的作者也考虑到不正确的裁剪,
因此将裁剪后模型损失最大的weight保留下来。
每裁剪完一层后,对于该层进行locally的fine-tune,locally的fine-tune,
是在每一层的filter上,使用最小二乘优化的方法来使裁剪后的filter
调整到使得输出与原始输出尽可能的接近。在所有层都裁剪完毕后,
再通过一个global的finetuning来恢复整体的性能。
f.遗传算法思想,随机剪裁,选择效果好的 论文参考
作者认为,既然我无法直观上的判定filter的重要性,
那么就采取一种随机裁剪的方式,然后对于每一种随机方式统计模型的性能,来确定局部最优的裁剪方式。
这种随机裁剪方式类似于一个随机mask,假设有M个潜在的可裁剪weight,那么一共就有2^M个随机mask。
假设裁剪比例为a,那么每层就会随机选取ML*a个filter,一共随机选取N组组合,
然后对于这N组组合,统计裁剪掉它们之后模型的性能,
然后选取性能最高的那组作为局部最优的裁剪方式。
g.基于icc组内相关来衡量filter的重要性 论文参考
作者发现,在最后一个卷积层中,经过LDA分析发现对于每一个类别,
有很多filter之间的激活是高度不相关的,
因此可以利用这点来剔除大量的只具有少量信息的filter而不影响模型的性能。
作者在VGG-16上进行实验,VGG-16的conv5_3具有512个filter,
将每一个filter的输出值中的最大值定义为该filter的fire score,
因此对应于每一张图片就具有一个512维的fire向量,当输入一堆图片时,
就可以得到一个N*512的fire矩阵,作者用intra-class correlation来衡量filter的重要性:
作者这样做的目的是通过只保留对分类任务提取特征判别性最强的filter,来降低模型的冗余。
h.基于神经元激活相关性的重要性判别方法 论文参考
作者认为,如果一层中的某个神经元的激活与上一层的某个神经元的激活有很强的相关性,
那么这个神经元对于后面层的激活具有很强的判别性。
也就是说,如果前后两层中的某对神经元的激活具有较高的相关性,
那么它们之间的连接weight就是非常重要的,而弱的相关性则代表低的重要性。
如果某个神经元可以视为某个特定视觉模式的探测器,那么与它正相关的神经元也提供了这个视觉模式的信息,
而与它负相关的神经元则帮助减少误报。作者还认为,那些相关性很低的神经元对,
它们之间的连接不一定是一点用也没有,它们可能是对于高相关性神经元对的补充。
i.将裁剪问题当做一个组合优化问题 论文参考
作者将裁剪问题当做一个组合优化问题:从众多的权重参数中选择一个最优的组合B,使得被裁剪的模型的代价函数的损失最小.
这类似于Oracle pruning的方式,即通过将每一个weight单独的剔除后看模型损失函数的衰减,
将衰减最少的参数认为是不重要的参数,可以剔除,这也是OBD的思路,但是OBD的方法需要求二阶导数,
实现起来难度较大,而本文提出的Taylor expansion的方法可以很好的解决这个问题.
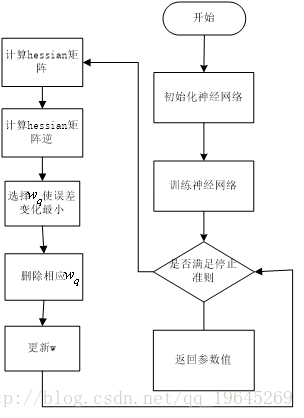
j. 一种基于Hessian矩阵的网络修剪算法
论文参考
OBS算法是一种基于Hessian矩阵的网络修剪算法,首先,构造误差曲面的一个局部模型,分析权值的扰动所造成的影响。 通过对误差函数进行Taylor展开
可以得到 与二阶导数 海塞矩阵H相关的一个式子
1.OBS算法的全称为optimal brain surgeon,翻译成中文就是最优外科手术,表面的意思就是该方法是和神经网络过程是分开的。
2.该方法是一种框架,只要是模型能求出参数的梯度,那么都可用这个方法进行稀疏化。
2. 量化(Quantization)
对象:对权重量化,对特征图量化(神经元输出),对梯度量化(训练过程中)
过程:在inference网络前传,在训练过程(反传)
一步量化(仅对权重量化),
两步量化(对神经元与特征图量化,第一步先对feature map进行量化,第二步再对权重量化)
32位浮点和16位浮点存储的时候,
第一位是符号位,中间是指数位,后面是尾数。
英特尔在NIPS2017上提出了把前面的指数项共享的方法,
这样可以把浮点运算转化为尾数的整数定点运算,从而加速网络训练。 
分布式训练梯度量化: 
在很多深度学习训练过程中,为了让训练更快往往会用到分布式计算。
在分布式计算过程中有一个很大问题,
每一个分布式服务器都和中心服务器节点有大量的梯度信息传输过程,从而造成带宽限制。
这篇文章采取把要传输的梯度信息量化为三值的方法来有效加速分布式计算。
聚类量化,降低内存消耗,但不能降低计算消耗
为了进一步压缩网络,考虑让若干个权值共享同一个权值,
这一需要存储的数据量也大大减少。
在论文中,采用kmeans算法来将权值进行聚类,
在每一个类中,所有的权值共享该类的聚类质心,
因此最终存储的结果就是一个码书和索引表。
1.对权值聚类
论文中采用kmeans聚类算法,
通过优化所有类内元素到聚类中心的差距(within-cluster sum of squares )来确定最终的聚类结果.
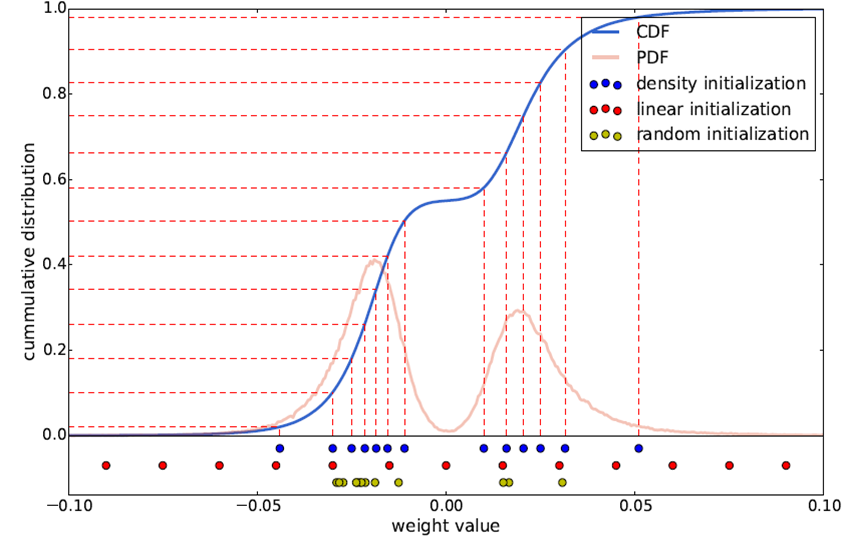
2. 聚类中心初始化
常用的初始化方式包括3种:
a) 随机初始化。
即从原始数据种随机产生k个观察值作为聚类中心。
b) 密度分布初始化。
现将累计概率密度CDF的y值分布线性划分,
然后根据每个划分点的y值找到与CDF曲线的交点,再找到该交点对应的x轴坐标,将其作为初始聚类中心。
c) 线性初始化。
将原始数据的最小值到最大值之间的线性划分作为初始聚类中心。
三种初始化方式的示意图如下所示:
由于大权值比小权值更重要(参加HanSong15年论文),
而线性初始化方式则能更好地保留大权值中心,
因此文中采用这一方式,
后面的实验结果也验证了这个结论。
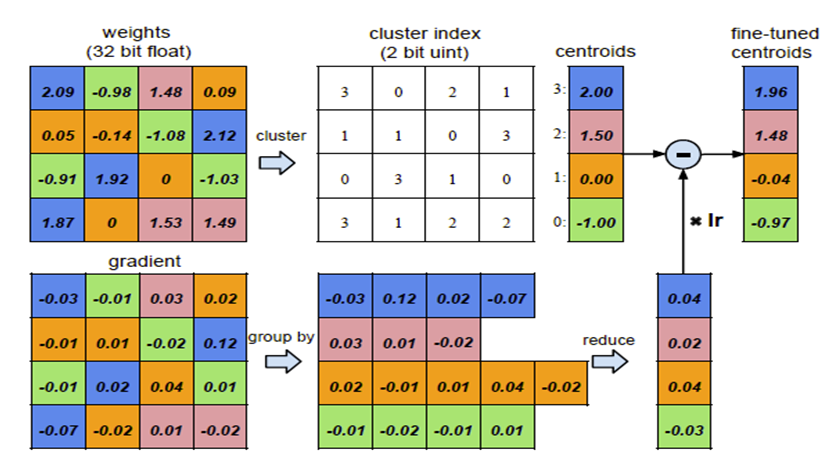
3. 前向反馈和后项传播
前向时需要将每个权值用其对应的聚类中心代替,
后向计算每个类内的权值梯度,
然后将其梯度和反传,
用来更新聚类中心,
如图:
共享权值后,就可以用一个码书和对应的index来表征。
假设原始权值用32bit浮点型表示,量化区间为256,
即8bit,共有n个权值,量化后需要存储n个8bit索引和256个聚类中心值,
则可以计算出压缩率compression ratio:
r = 32*n / (8*n + 256*32 )≈4
可以看出,如果采用8bit编码,则至少能达到4倍压缩率。
2. 二值量化网络

上图是在定点表示里面最基本的方法:BNN和BWN。
在网络进行计算的过程中,可以使用定点的数据进行计算,
由于是定点计算,实际上是不可导的,
于是提出使用straight-through方法将输出的估计值直接传给输入层做梯度估计。
在网络训练过程中会保存两份权值,用定点的权值做网络前向后向的计算,
整个梯度累积到浮点的权值上,整个网络就可以很好地训练,
后面几乎所有的量化方法都会沿用这种训练的策略。
前面包括BNN这种网络在小数据集上可以达到跟全精度网络持平的精度,
但是在ImageNet这种大数据集上还是表现比较差。 **1. BCN & BNN 全二值网络** [Binarized Neural Networks BNN](https://arxiv.org/pdf/1602.02830.pdf)
BNN的激活量和参数都被二值化了, 反向传播时使用全精度梯度。
有确定性(sign()函数)和随机(基于概率)两种二值化方式。
使用sign函数时,sign函数不可导,使用直通估计(straight-through estimator)(即将误差直接传递到下一层): ….
gr=gq1|r|≤1
BNN中同时介绍了基于移位(而非乘法)的BatchNormailze和AdaMax算法。
实验结果:
在MNIST,SVHN和CIFAR-10小数据集上几乎达到了顶尖的水平。
在ImageNet在使用AlexNet架构时有较大差距(在XNOR-Net中的实验Δ=29.8%)
在GPU上有7倍加速 **2. BWN(Binary-Weights-Networks) 仅有参数二值化了,激活量和梯度任然使用全精度**
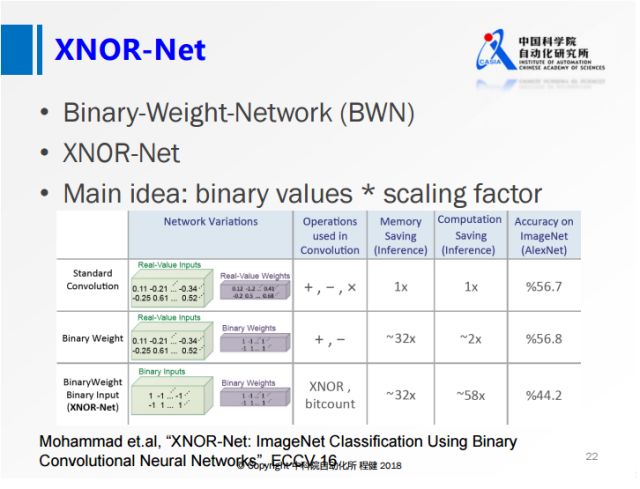
上图展示了ECCV2016上一篇名为XNOR-Net的工作,
其思想相当于在做量化的基础上,乘了一个尺度因子,这样大大降低了量化误差。
他们提出的BWN,在ImageNet上可以达到接近全精度的一个性能,
这也是首次在ImageNet数据集上达到这么高精度的网络。
该网络主要是对W 进行二值化,主要是一些数学公式的推导,公式推导如下:
对W进行二值化,使用 B 和缩放比例 a 来近似表达W 
全精度权重W 和 加权二进制权重 aB 的误差函数,求解缩放比例a和二值权重B,使得误差函数值最小 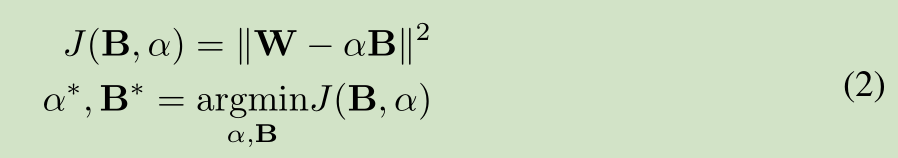
误差函数展开 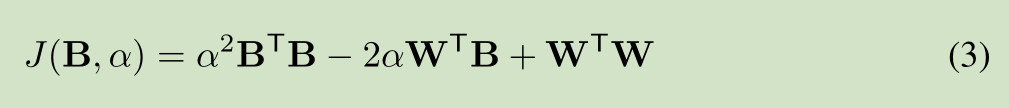
二值权重B的求解,误差最小,得到 W转置*B最大 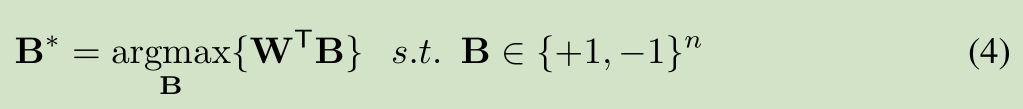
缩放比例a的求解,由全精度权重W求解得到 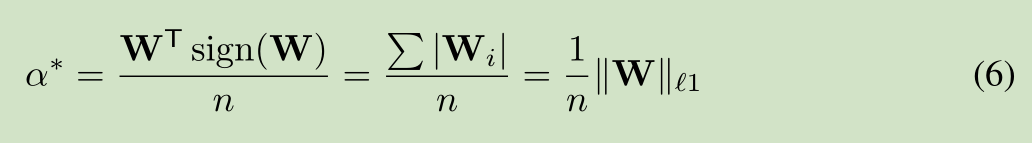
3. XNOR-Net是BinaryNet的升级版
主要思想:
1. 二值化时增加了缩放因子,同时梯度函数也有相应改变:
W≈W^=αB=1n∑|W|ℓ1×sign(W)
∂C∂W=∂C∂W^(1n+signWα)
2. XNOR-Net在激活量二值化前增加了BN层
3. 第一层与最后一层不进行二值化
实验结果:
在ImageNet数据集AlexNet架构下,BWN的准确率有全精度几乎一样,XNOR-Net还有较大差距(Δ=11%)
减少∼32×的参数大小,在CPU上inference阶段最高有∼58× 的加速。
**4. 量化网络 nbit量化 **
对BNN的简单扩展,
量化激活函数,
有线性量化与log量化两种,
其1-bit量化即为BinaryNet。
在正向传播过程中加入了均值为0的噪音。
BNN约差于XNOR-NET(<3%),
QNN-2bit activation 略优于DoReFaNet 2-bit activation
激活函数量 线性量化:
LinearQuant(x, bitwidth)= Clip(round(x/bitwidth)*bitwidth, minV, maxV )
激活函数为 整数阶梯函数
最小值 minV
最大值 maxV
中间 线性阶梯整数
log量化:
LogQuant(x, bitwidth)、 = Clip (AP2(x), minV, maxV )
AP2(x) = sign(x) × 2^round(log2|x|)
平方近似
5. 约束低比特(3比特)量化 Extremely Low Bit Neural Networks
论文 Extremely Low Bit Neural Network: Squeeze the Last Bit Out with ADMM
ADMM 算法理解 对原函数不好求解,转而求解它的对偶函数,基于对对偶函数的优化,从来解出原问题

上图展示了阿里巴巴冷聪等人做的通过ADMM算法求解binary约束的低比特量化工作。
从凸优化的角度,在第一个优化公式中,f(w)是网络的损失函数,
后面会加入一项W在集合C上的loss来转化为一个优化问题。
这个集合C取值只有正负1,如果W在满足约束C的时候,它的loss就是0;
W在不满足约束C的时候它的loss就是正无穷。
为了方便求解还引进了一个增广变量,保证W是等于G的,
这样的话就可以用ADMM的方法去求解。
提出一种基于低比特表示技术的神经网络压缩和加速算法。
我们将神经网络的权重表示成离散值,
并且离散值的形式为 2 的幂次方的形式,比如 {-4,-2,-1,0,1,2,4}。
这样原始 32 比特的浮点型权重可以被压缩成 1-3 比特的整形权重,
同时,原始的浮点数乘法操作可以被定点数的移位操作所替代。
在现代处理器中,定点移位操作的速度和能耗是远远优于浮点数乘法操作的。
{-1,0,1 }, 三值网络,存储只需要2bit,极大地压缩存储空间,
同时也可以避免乘法运算,只是符号位的变化和加减操作,从而提升计算速度。 
{-2,-1,0,1,2}, 五值网络 和 {-4,-2,-1,0,1,2,4} 七值网络,
需要3bit存储
首先,我们将离散值权重的神经网络训练定义成一个离散约束优化问题。
以三值网络为例,其目标函数可以表示为: 
在约束条件中引入一个 scale(尺度)参数。
对于三值网络,我们将约束条件写成 {-a, 0, a}, a>0.
这样做并不会增加计算代价,
因为在卷积或者全连接层的计算过程中可以先和三值权重 {-1, 0, 1} 进行矩阵操作,
然后对结果进行一个标量 scale。
从优化的角度看,增加这个 scale 参数可以大大增加约束空间的大小,
这有利于算法的收敛。如下图所示: 
对于三值网络而言,scale 参数可以将约束空间从离散的 9 个点扩增到 4 条直线。
为了求解上述约束优化问题,我们引入 ADMM 算法。
在此之前,我们需要对目标函数的形式做一个等价变换(对偶变换)。 

其中 Ic 为指示函数,
如果 G 符合约束条件,则 Ic(G)=0,
否则 Ic(G) 为无穷大。
该目标函数的增广拉格朗日形式为( 将条件 引入到 目标函数): 
ADMM 算法将上述问题分成三个子问题进行求解,即: 
与其它算法不同的是,我们在实数空间和离散空间分别求解,
然后通过拉格朗日乘子的更新将两组解联系起来。
第一个子问题需要找到一个网络权重最小化 
在实验中我们发现使用常规的梯度下降算法求解这个问题收敛速度很慢。
在这里我们使用 Extra-gradient 算法来对这个问题进行求解。
Extra-gradient 算法包含两个基本步骤,分别是: 
第二个子问题在离散空间中进行优化。通过简单的数学变换第二个子问题可以写成: 
该问题可以通过迭代优化的方法进行求解。当 a 或 Q 固定时,很容易就可以获得 Q 和 a 的解析解。
除上述三值网络外,还有以下几种常用的参数空间: 
参数空间中加入2、4、8等值后,仍然不需要乘法运算,只需进行移位操作。
因此,通过这种方法将神经网络中的乘法操作全部替换为移位和加操作。
6. 哈希函数两比特缩放量化 BWNH 论文

保留内积哈希方法是沈老师团队在15年ICCV上提出的 Learning Binary Codes for Maximum Inner Product Search
通过Hashing方法做的网络权值二值化工作。
第一个公式是我们最常用的哈希算法的公式,其中S表示相似性,
后面是两个哈希函数之间的内积。
我们在神经网络做权值量化的时候采用第二个公式,
第一项表示输出的feature map,其中X代表输入的feature map,W表示量化前的权值,
第二项表示量化后输出的feature map,其中B相当于量化后的权值,
通过第二个公式就将网络的量化转化成类似第一个公式的Hashing方式。
通过最后一行的定义,就可以用Hashing的方法来求解Binary约束。
本文在二值化权重(BWN)方面做出了创新,发表在AAAI2018上,作者是自动化所程建团队。
本文的主要贡献是提出了一个新的训练BWN的方法,
揭示了哈希与BW(Binary Weights)之间的关联,表明训练BWN的方法在本质上可以当做一个哈希问题。
基于这个方法,本文还提出了一种交替更新的方法来有效的学习hash codes而不是直接学习Weights。
在小数据和大数据集上表现的比之前的方法要好。
为了减轻用哈希方法所带来的loss,
本文将binary codes乘以了一个scaling factor并用交替优化的策略来更新binary codes以及factor.
3. 三值化网络
TNN 全三值网络
训练时激活量三值化,参数全精度
infernce时,激活量,参数都三值化(不使用任何乘法)
用FPGA和ASIC设计了硬件 ## TWN 三值系数网络
权值三值化的核心:
首先,认为多权值相对比于二值化具有更好的网络泛化能力。
其次,认为权值的分布接近于一个正态分布和一个均匀分布的组合。
最后,使用一个 scale 参数去最小化三值化前的权值和三值化之后的权值的 L2 距离。
算法 
这个算法的核心是只在前向和后向过程中使用使用权值简化,但是在update是仍然是使用连续的权值。
简单的说就是先利用公式计算出三值网络中的阈值: 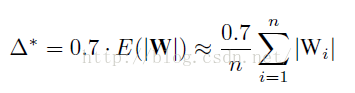
也就是说,将每一层的权值绝对值求平均值乘以0.7算出一个deta作为三值网络离散权值的阈值,
具体的离散过程如下: 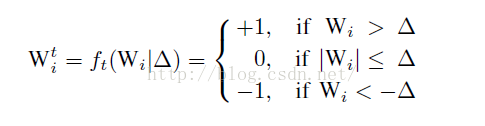
其实就是简单的选取一个阈值(Δ),
大于这个阈值的权值变成 1,小于-阈值的权值变成 -1,其他变成 0。
当然这个阈值其实是根据权值的分布的先验知识算出来的。
本文最核心的部分其实就是阈值和 scale 参数 alpha 的推导过程。
在参数三值化之后,作者使用了一个 scale 参数去让三值化之后的参数更接近于三值化之前的参数。
根据一个误差函数 推导出 alpha 再推导出 阈值(Δ)
这样,我们就可以把连续的权值变成离散的(1,0,-1),
那么,接下来我们还需要一个alpha参数,具体干什么用后面会说(增强表达能力)
这个参数的计算方式如下: 
|I(deta)|这个参数指的是权值的绝对值大于deta的权值个数,计算出这个参数我们就可以简化前向计算了,
具体简化过程如下: 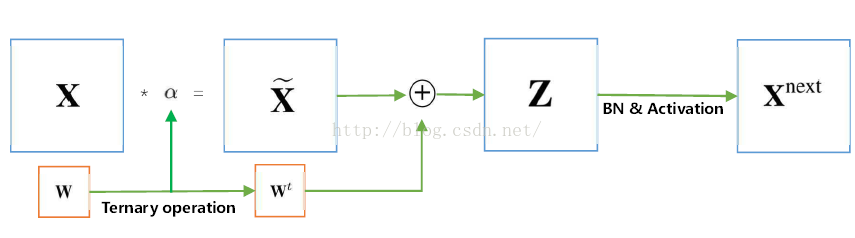
可以看到,在把alpha乘到前面以后,我们把复杂的乘法运算变成了简单的加法运算,从而加快了整个的训练速度。
主要思想就是三值化参数(激活量与梯度精度),参照BWN使用了缩放因子。
由于相同大小的filter,
三值化比二值化能蕴含更多的信息,
因此相比于BWN准确率有所提高。
训练三值量化 TTQ 训练浮点数量化
Trained Ternary Quantization TTQ
提供一个三值网络的训练方法。
对AlexNet在ImageNet的表现,相比32全精度的提升0.3%。
与TWN类似,
只用参数三值化(训练得到的浮点数),
但是正负缩放因子不同,
且可训练,由此提高了准确率。
ImageNet-18模型仅有3%的准确率下降。
对于每一层网络,三个值是32bit浮点的{−Wnl,0,Wpl},
Wnl、Wpl是可训练的参数。
另外32bit浮点的模型也是训练的对象,但是阈值Δl是不可训练的。
由公式(6)从32bit浮点的到量化的三值: 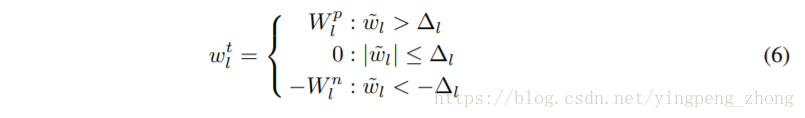
由(7)算出Wnl、Wpl的梯度: 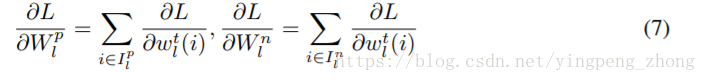
其中: 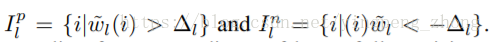
由(8)算出32bit浮点模型的梯度 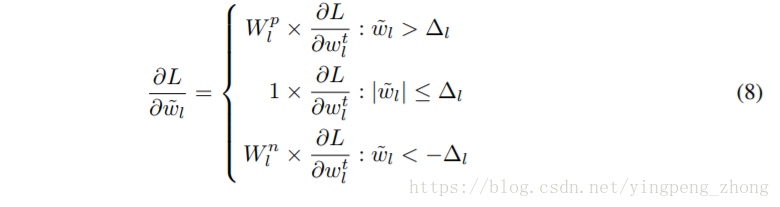
由(9)给出阈值,这种方法在CIFAR-10的实验中使用阈值t=0.05。
而在ImageNet的实验中,并不是由通过钦定阈值的方式进行量化的划分,
而是钦定0值的比率r,即稀疏度。 
整个流程: 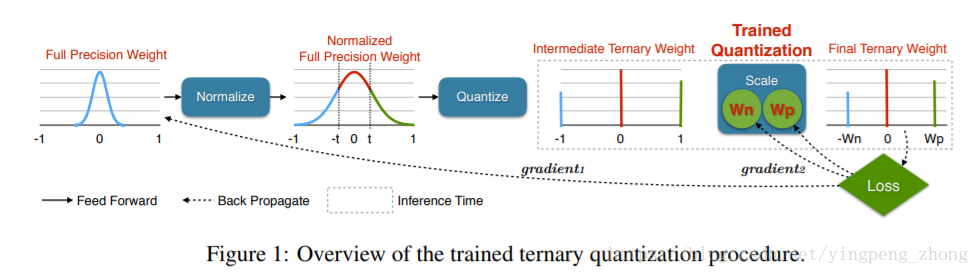
三值 矩阵分解和定点变换
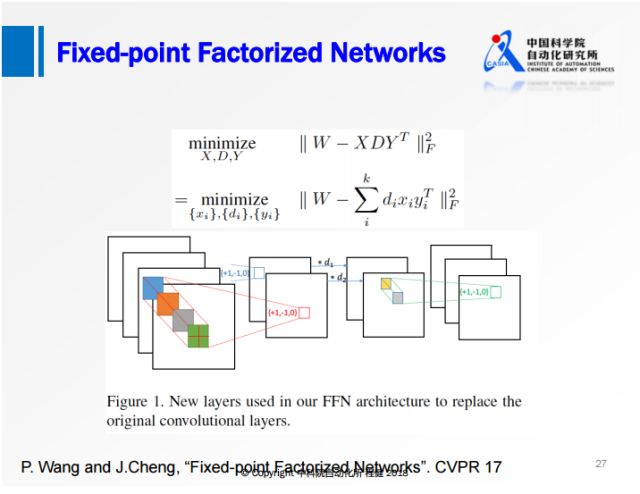
借助了矩阵分解和定点变换的优势,
对原始权值矩阵直接做一个定点分解,限制分解后的权值只有+1、-1、0三个值。
将网络变成三层的网络,首先是正常的3×3的卷积,对feature map做一个尺度的缩放,
最后是1×1的卷积,所有的卷积的操作都有+1、-1、0。
4. 二进制位量化网络 哈希函数的味道啊 ShiftCNN
一个利用低精度和量化技术实现的神经网络压缩与加速方案。
最优量化
量化可以看作用离散码本描述样本分布。
优化目标(最大概率准则)和优化方法(L1和L2正则化)通常导致了神经网络参数呈现中心对称的非均匀分布。
因此,一个最佳的量化码本应当是一个非均匀分布的码本。
这也是为什么BinaryNet(-1,+1)、ternary quantization(-1,0,+1)这种策略性能不足的一个重要原因。
需要注意的是,
量化之前需要对参数进行范围归一化,
即除以最大值的绝对值,这样保证参数的绝对值都小于1。
该量化方法具有码本小、量化简单、量化误差小的优点。
量化
ShiftCNN所采用是一种相当巧妙的类似于残差量化的方法。
完整的码本包含 N 个子码本。
每个码本包含 M=2^B−1 个码字,即每一个码字可以用 B bit 表示。
每个码本定义如下:
Cn=0, ±2^−n+1, ±2^−n, …, ±2^−n−⌊M/2⌋+2
假设 N=2,B=4,则码本为
C1=0, ±2^−1, ±2^−2, ±2^−3, ±2^−4, ±2^−5, ±2^−6
C2=0, ±2^−2, ±2^−3, ±2^−4, ±2^−5, ±2^−6, ±2^−7
于是,每一个权重都可以使用 N*B bit 的索引通过下式求和计算得到:
wi' = sum(Cn[id(n)])
卷积计算
卷积计算的复杂度主要来自乘法计算。
ShiftCNN采用简单的移位和加法来实现乘法,从而减少计算量。
比如计算 y=wx, 而 w 通过量化已经被我们表示成了,
类似于 2^−1 + 2^−2 + 2^−3 这种形式,
于是 y = x>>1 + x>>2 + x>>3
3. 编码(Huffman Encoding)
4. 迁移学习方法 基于教师——学生网络的方法
基于教师——学生网络的方法,属于迁移学习的一种。
迁移学习也就是将一个模型的性能迁移到另一个模型上,
而对于教师——学生网络,教师网络往往是一个更加复杂的网络,
具有非常好的性能和泛化能力,
可以用这个网络来作为一个soft target来指导另外一个更加简单的学生网络来学习,
使得更加简单、参数运算量更少的学生模型也能够具有和教师网络相近的性能,
也算是一种模型压缩的方式。
a. Distilling the Knowledge in a Neural Network 论文参考
较大、较复杂的网络虽然通常具有很好的性能,
但是也存在很多的冗余信息,因此运算量以及资源的消耗都非常多。
而所谓的Distilling就是将复杂网络中的有用信息提取出来迁移到一个更小的网络上,
这样学习来的小网络可以具备和大的复杂网络想接近的性能效果,并且也大大的节省了计算资源。
这个复杂的网络可以看成一个教师,而小的网络则可以看成是一个学生。
这个复杂的网络是提前训练好具有很好性能的网络,
学生网络的训练含有两个目标:
一个是hard target,即原始的目标函数,为小模型的类别概率输出与label真值的交叉熵;
另一个为soft target,为小模型的类别概率输出与大模型的类别概率输出的交叉熵.
在soft target中,概率输出的公式调整如下,
这样当T值很大时,可以产生一个类别概率分布较缓和的输出
作者认为,由于soft target具有更高的熵,它能比hard target提供更加多的信息,
因此可以使用较少的数据以及较大的学习率。
将hard和soft的target通过加权平均来作为学生网络的目标函数,
soft target所占的权重更大一些。
作者同时还指出,T值取一个中间值时,效果更好,
而soft target所分配的权重应该为T^2,hard target的权重为1。
这样训练得到的小模型也就具有与复杂模型近似的性能效果,但是复杂度和计算量却要小很多。
对于distilling而言,复杂模型的作用事实上是为了提高label包含的信息量。
通过这种方法,可以把模型压缩到一个非常小的规模。
模型压缩对模型的准确率没有造成太大影响,而且还可以应付部分信息缺失的情况。
b.使用复杂网络中能够提供视觉相关位置信息的Attention map来监督小网络的学习
论文参考
代码
作者借鉴Distilling的思想,
使用复杂网络中能够提供视觉相关位置信息的Attention map来监督小网络的学习,
并且结合了低、中、高三个层次的特征.
教师网络从三个层次的Attention Transfer对学生网络进行监督。
其中三个层次对应了ResNet中三组Residual Block的输出。
在其他网络中可以借鉴。
这三个层次的Attention Transfer基于Activation,
Activation Attention为feature map在各个通道上的值求和,
但是就需要两次反向传播的过程,实现起来较困难并且效果提升不明显。
基于Activation的Attention Transfer效果较好,而且可以和Hinton的Distilling结合。
模型压缩总结
1. 核参数稀疏
在损失函数中添加使得参数趋向于稀疏的项,
使得模型在训练过程中,其参数权重趋向于稀疏。
2. 权重矩阵低秩分解
核心思想就是把较大的卷积核分解为两个级联的行卷积核和列卷积核,
例如 3*3卷积分成 1*3卷积和 3*1卷积 级联。
这里对于1*1的卷积核无效。
3. 剪枝
可分为在filter级别上剪枝或者在参数级别上剪枝:
a. 对于单个filter,有阈值剪枝方法,将filter变得稀疏。
b. 宏观上使用一种评价方法(能量大小)来计算每个filter的重要性得分,
去除重要性低的filter。
4. 量化
a. 降低数据数值范围
单精度浮点数(32)-> 半精度浮点数(16)
->无符号(8) -> 三值 -> 二值
b. 聚类编码实现权值共享的方法
对卷积核参数进行k_means聚类,得到聚类中心。,
对原始参数,使用其所属的中心id来代替。
然后通过储存这k个类别的中心值,以及id局矩阵来压缩网络。
5. 迁移学习
通过将较大较复杂较优秀的网络(老师)中的有用信息提取出来迁移到一个更小的网络上(学生),
这样学习来的小网络可以具备和大的复杂网络相想接近的性能效果,实现网络的压缩。
转载请注明原地址,万有文的博客:ewenwan.github.io谢谢!